Algoritmo di Stålmarck

Formula con congiunzioni ed equivalenze

Possiamo esprimere tutte le formule in termini dei soli connettori ¬, ∧, ≡:: x∨y equivalente a ¬(¬x∧¬y)
x⇒y equivalente a ¬(x∧¬y)

Esempi

Tradurre la formula ((v1⇒v2)∧(v3⇒v4))⇒((v1∧v3)⇒(v2∧v4)):: Espandere le implicazioni: ¬((¬(v1∧¬v2)∧¬(v3∧¬v4))∧((v1∧v3)∧¬(v2∧v4)))

Esercizi

D1 Scrivere una funzione transform che cambia le disgiunzioni e le implicazioni con le formule equivalenti.

Tripla

Una formula può essere rappresentata sotto forma di albero:

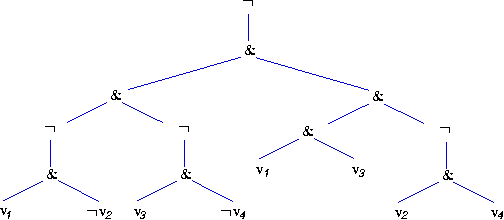
Ad ogni nodo binario dell'albero si può associare una nuova variabile:

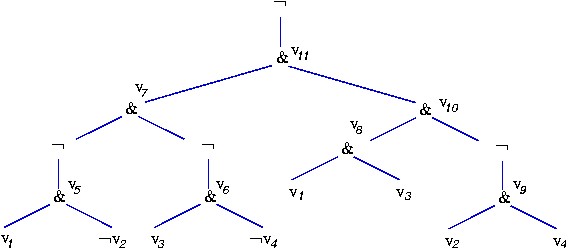
Cosí ogni nuova variabile forma una tripla:

v11=v7∧v10
v10=v8∧¬v9
v9=v2∧v4
v8=v1∧v3
v7=¬v5∧¬v6
v6=v3∧¬v4
v5=v1∧¬v2

Il valore della formula iniziale è quello di ¬v11.

Esercizi

D2 Scrivere una funzione make_triplets che trasforma una formula in una lista di triple.

Propagazione

Conoscendo i valori relativi di alcune variabili di una tripla, si possono dedurre nuovi fatti sui valori di altre variabili.

Tripla congiuntiva

Abbiamo v1= v2 ∧ v3:

Se v1=true allora v2=v3=true.
Se v2=true allora v1=v3.
Se v2=false allora v1=false.
Se v3=true allora v1=v2.
Se v3=false allora v1=false.
Se v1=¬v2 allora v1=v3=false.
Se v1=¬v3 allora v1=v2=false.
Se v2=v3 allora v1=v2.
Se v2=¬v3 allora v1=false.

Tripla equivalente

Abbiamo v1= v2 ≡ v3:

Se v1=true allora v2=v3.
Se v1=false allora v2=¬v3.
Se v2=true allora v1=v3.
Se v2=false allora v1=¬v3.
Se v3=true allora v1=v2.
Se v3=false allora v1=¬v2.
Se v1=v2 allora v3=true.
Se v1=¬v2 allora v3=false.
Se v1=v3 allora v2=true.
Se v1=¬v3 allora v2=false.
Se v2=v3 allora v1=true.
Se v2=¬v3 allora v1=false.

Propagazione

Le regole delle triple permettono di aggiungere nuove equazioni che possono essere utilizzate a loro volta. Questo meccanismo ricorsivo si chiama propagazione.

Refutazione

Nel processo di propagazione si parte da un ambiente iniziale (una collezione di equazioni) e si aggiungono nuove equazioni. Può capitare che una nuova equazione sia in contraddizione con il suo ambiente. Per esempio, la regola 1 della tripla equivalente dice di aggiungere l'equazione v1=v2 ma forse abbiamo già nell'ambiente che v1=¬v2. Il fatto di avere una contraddizione vuole semplicemente dire che l'ambiente iniziale era impossibile.

Il fatto che le contraddizioni siano possibili dà un metodo per provare le tautologie. Si può assumere nell'ambiente iniziale che la formula è falsa e se usando la propagazione risulta una contraddizione, si può concludere che la formula è una tautologia.

Questo metodo è sufficiente per provare che il nostro esempio è una tautologia. Neghiamo la variabile che rappresenta la formula ¬v11=false

Da v11=true con la tripla 1 e la regola 1, segue v7=true e v10=true
Da v10=true con la tripla 2 e la regola 1, segue v8=true e v9=false
Da v8=true con la tripla 4 e la regola 1, segue v1=true e v3=true
Da v7=true con la tripla 5 e la regola 1, segue v5=false e v6=false
Da v5=false e v1=true con la tripla 7 e la regola 6, segue v2=true
Da v6=true e v3=true con la tripla 6 e la regola 6, segue v4=true
Da v2=true e v4=true con la tripla 3 e la regola 8, segue v9=true
Da v9=true e v9=false, segue una contraddizione.

Esercizi

D3. Definire un tipo di dato per rappresentare l'ambiente (la collezione di equazioni). Su tale tipo, definire le funzioni:

get_min che, data una variabile segnata, restituisce la variabile di indice più piccolo uguale alla variabile data.
get_class che, data una variabile segnata, restituisce la lista delle variabili uguali alla variabile data.
add_eq che permette di aggiungere una equazione.
is_contradictory che verifica che c'è una contraddizione nell'ambiente.

D4. Scrivere una funzione propagate che prende un ambiente e due variabili v1 e v2 e fa la propagazione dell'equazione v1=v2.

Dilemma

Regola del dilemma

La vera originalità dell'algoritmo di Stålmarck consiste nel non fare un'esplorazione esponenziale. Si creano due rami sui quali si fa la propagazione. A questo punto non si itera ma si calcola semplicemente l'intersezione:

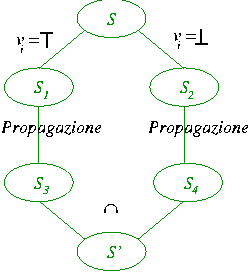
Sappiamo che S3 contiene S ed S4 contiene S. Dunque l'intersezione contiene almeno S: si può solo guadagnare informazione.

Se S3 è una contraddizione, allora l'intersezione è S4.

Se S4 è una contraddizione, allora l'intersezione è S3.

Se S3 e S4 sono contraddizioni, allora l'intersezione è una contraddizione.

Iterazione

Si può fare un'iterazione dell'applicazione della regola del dilemma su tutte le variabili possibili fino a quando non vi sia una nuova informazione da guadagnare:

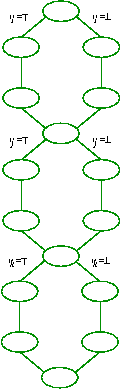
Ricorsione

Finalmente si può usare l'iterazione precedente in maniera ricorsiva usando un livello di profondità n. Dopo la creazione dei rami, se n vale 1, usiamo la propagazione (come descritta nella regola del dilemma). Se n non vale 1, usiamo la stessa iterazione ma questa volta al livello n-1. Per esempio per n=2 abbiamo:

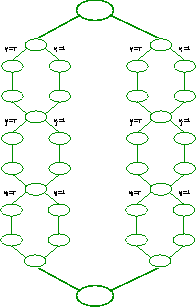
La proprietà interessante è che n=2 è normalmente sufficiente per sapere se la formula è una tautologia. Se usiamo n=numero di variabili, questo algoritmo è equivalente a quello di Davis.

Esempio

Prendiamo la formula

(v1 ∧ v2) ∨ ((v1 ∧ ¬v2) ∨ ((¬v1 ∧ v2) ∨ ((¬v1 ∧ ¬v2))))

Espandiamo le congiunzioni:

¬(¬(v1 ∧ v2) ∧ (¬(v1 ∧ ¬v2) ∧ (¬(¬v1 ∧ v2) ∧ ¬(¬v1 ∧ ¬v2))))

La lista delle triple è:

v9=¬v3∧v8
v8=¬v4∧v7
v7=¬v5∧¬v6
v6=¬v1∧¬v2
v5=¬v1∧v2
v4=v1∧¬v2
v3=v1∧v2

Il valore della formula iniziale è quello di ¬v9. Partiamo di ¬v9=false. La propagazione non permette di concludere:

Da v9=true con la tripla 1 e la regola 1, segue v3=false e v8=true
Da v8=true con la tripla 2 e la regola 1, segue v4=false e v7=true
Da v7=true con la tripla 3 e la regola 1, segue v5=false e v6=false

Alla fine sappiamo che

v9=v8=v7=true e v6=v5=v4=v3=false. Per concludere bisogna fare una dilemma su v1.

Caso v1=true

Da v3=false e v1=true con la tripla 7 e la regola 6, segue v2=false
Da v4=false e v1=true con la tripla 6 e la regola 6, segue v2=true dunque una contraddizione

Caso v1=false

Da v5=false e v1=true con la tripla 5 e la regola 6, segue v2=true
Da v6=false e v1=true con la tripla 4 e la regola 6, segue v2=false dunque una contraddizione

L'intersezione di una contraddizione e una contraddizione è una contraddizione. Abbiamo una contraddizione. Dunque la formula initiale è una tautologia.

Esercizi

D5. Scrivere una funzione get_intersect che calcola l'intersezione di due ambienti.

D6, Scrivere una funzione stal che, dati un livello d'iterazione ed una formula, utilizza l'algoritmo di Stålmarck per sapere se la formula è una tautologia.

Laurent Théry

Last modified: Tue Apr 30 01:38:21 MEST 2002