Algoritmo di Davis-Putnam
Formula in forma CNF
Equivalenze
-
Possiamo esprimere tutte le formule in termini
dei soli connettori ¬, ∧, ∨:
-
x⇒y equivalente a ¬x∨y
x≡y equivalente a (x∨¬y)∧(¬x∨y)
Ordine
Una formula è in forma CNF (conjunctive normal form) se comincia
con le congiunzioni, dopo le disgiunzioni e infine le negazioni. Ovvero,
è una congiunzione di disgiunzioni di variabili eventualmente
negate.
(x∨¬y)∧(¬x∨y) è in forma CNF
(x∧¬y)∨(¬x∧y) non lo è
Trasformazione
Tutte le formule possono essere messe in forma CNF.
-
Primo passo: si possono mettere dentro le negazioni:
-
¬(x∧y) equivalente a ¬x∨¬y
¬(x∨y) equivalente a ¬x∧¬y
¬(¬x) equivalente a x
-
Secondo passo: si possono mettere le congiunzioni prima delle disgiunzioni:
-
x∨(y∧z) equivalente a (x∨y)∧(x∨z)
(y∧z)∨x equivalente a (y∨x)∧(z∨x)
Esempi
Mettere la formula (x∨y)⇒z in forma CNF:
- Espandere l'implicazione: ¬(x∨y)∨z
- Mettere in fondo le negazioni: (¬x∧¬y)∨z
- Mettere le congiunzioni prima delle disgiunzioni: (¬x∨z)∧(¬y∨z)
Mettere la formula (x⇒y)⇒(z⇒t) in forma CNF:
- Espandere l'implicazione: ¬(¬x∨y)∨(¬z∨t)
- Mettere in fondo le negazioni: (x∧¬y)∨(¬z∨t)
- Mettere le congiunzioni prima delle disgiunzioni: (x∨¬z∨t)∧(¬y∨¬z∨t)
Esercizi
C1
Scrivere una funzione expand che cambia le implicazioni e le equivalenze con le formule equivalenti.
C2
Scrivere una funzione check_cnf che verifica se una formula di tipo boolean è in forma CNF.
C3
Scrivere una funzione push_neg che, data una formula booleana contenente solo ∧,∨,¬, mette in fondo le negazioni.
C4
Scrivere una funzione push_or che, data una formula booleana contenente solo ∧,∨,¬, mette le disgiunzioni dopo le congiunzioni.
C5
Scrivere una funzione cnf che trasforma una formula booleana in una formula equivalente in forma CNF.
*C6
Mettere in forma CNF la formula (x∨¬y)⇒z.
Soddisfacibilità
Prendiamo un esempio con la formula (¬v1∨v3)∧(¬v1∨¬v2)∧(¬v3∨v2).
Con la tabella, abbiamo un'esecuzione cosí:
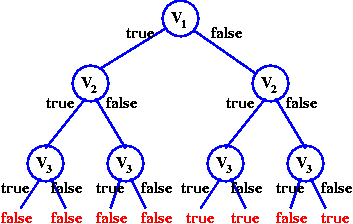
Contraddizione
Poiché la formula è in forma CNF, possiamo individuare
in anticipo quando la formula è falsa.
Nell'esempio precedente, una volta
che abbiamo v1=true e v2=true non è possibile
soddisfare la disgiunzione ¬v1∨¬v2. Si può
concludere senza considerare v3:
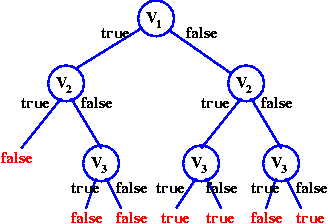
Risoluzione unitaria
In realtà si può fare di più. Una volta che abbiamo
v1=true, l'unica possibilità per verificare
¬v1∨¬v2 è d'avere v2=false. Anche
per verificare ¬v1∨v3 bisogna avere v3=true:
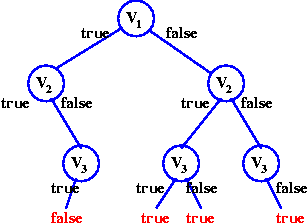
In una formula in forma CNF, le disgiunzioni contengono solo
variabili positive o negative (x o ¬x).
Se per una disgiunzione,
tutte le sue variabili segnate (positive o negative) sono false meno una,
quest'ultima deve essere vera.
Applicare questa regola ricorsivamente si chiama
risoluzione unitaria. Usare questa risoluzione nella ricerca
della soddisfacibilità è usare l'algoritmo di Davis-Putnam.
Con una implementazione semplice di questo algorithmo, si può
verificare la soddisfacibilità del problema delle N regine fino
a N=15.
Esercizi
C7
Scrivere una funzione eval_disj che valuta una formula
(composta unicamente di disgiunzioni, variabili e negazioni di variabili)
rispettivamente a una valutazione di alcune variabili, e dice
se la formula è vera o falsa o quali sono le variabili
della formula che non hanno valore nella valutazione data.
La valutazione può essere rappresentata come una lista.
I valori dentro questa lista sono vero, falso o sconosciuto.
C8
Scrivere una funzione eval_conj che prende una formula
in forma CNF e una valutazione e dice se per questa valutazione
la formula è vera, falsa, o ci sono candidati alla
risoluzione unitaria.
C9
Scrivere una funzione davis che implementa l'algoritmo di Davis-Putnam.
Laurent Théry
Last modified: Tue Apr 30 01:38:21 MEST 2002



