Definition InvTrans :  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R) (Trans E (Inv E R)) = (Trans E (Inv E R)) =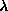 E:Set. E:Set.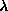 R:(Rel E). R:(Rel E).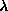 H:( H:( x,y,z:E.(R x y) x,y,z:E.(R x y) (R y z) (R y z) (R x z)). (R x z)).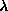 x,y,z:E. x,y,z:E.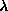 H0:(R y x). H0:(R y x).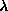 H1:(R z y).(H z y x H1 H0). H1:(R z y).(H z y x H1 H0). |
| Retour | Sommaire | Suite |
Revoyons le point de départ de notre traduction pour mieux apprécier le résultat final.
Definition InvTrans :  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R) (Trans E (Inv E R)) = (Trans E (Inv E R)) =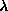 E:Set. E:Set.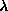 R:(Rel E). R:(Rel E).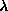 H:( H:( x,y,z:E.(R x y) x,y,z:E.(R x y) (R y z) (R y z) (R x z)). (R x z)).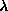 x,y,z:E. x,y,z:E.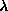 H0:(R y x). H0:(R y x).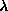 H1:(R z y).(H z y x H1 H0). H1:(R z y).(H z y x H1 H0). |
|
Théorème InvTrans. Énoncé :  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R) (Trans E (Inv E R)). (Trans E (Inv E R)).Proof : Considérons un ensemble E quelconque ; un terme R quelconque de type (Rel E) ; posons par hypothèse (Trans R E) (H). Considérons trois éléments x, y, et z quelconques de E ; posons par hypothèse (Inv E R x y) (H1) et (Inv E R y z) (H2). * Par l'hypothèse H2 nous avons (Inv E R y z) ce qui est équivalent à (R z y). * Par l'hypothèse H1 nous avons (Inv E R x y) ce qui est équivalent à (R y x). En appliquant l'hypothèse H nous obtenons (R z x). Nous avons montré  x,y,z:E.(R y x) x,y,z:E.(R y x) (R z y) (R z y) (R z x), ce qui est équivalent à (Trans E (Inv E R)). (R z x), ce qui est équivalent à (Trans E (Inv E R)).Nous avons montré  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R) (Trans E (Inv E R)). (Trans E (Inv E R)).Qed. |
J'espère que ce dernier texte vous semble compréhensible. Ce n'est sans doute pas le preuve telle qu'un mathématicien l'aurait écrite. Mais notre but est d'obtenir un texte qu'il puisse lire et comprendre. Passons maintenant à la
| Retour | Sommaire | Suite |