Résultats

Résultats et avancement du projet

Mots clefs: manipulation mobile, système non-holonôme, stabilisation, fonctions de tâches, fonctions transverses.

Projet ICARE de l'INRIA de Sophia Antipolis

Le contrôle des manipulateurs mobiles recouvre deux difficultés majeures:

La gestion des singularités et de la redondance.
Le traitement de la non-holonômie.

Nous avons donc décidé de traiter le cas plus simple d'un manipulateur mobile redondant holonôme, puis la commande de la base mobile non-holonôme, avant d'étudier la commande d'un manipulateur mobile redondant non-holonôme.

Traitement des singularités et de la redondance pour un manipulateur mobile holonôme.

Le formalisme des fonctions de tâches (1) donne un cadre méthodologique pour la commande des systèmes robotiques holonômes. Nous l'avons repris pour l'adapter, dans un premier temps, au problème de suivi d'un objet omnidirectionnel par un manipulateur mobile redondant et holonôme. La construction de la loi de commande peut se décomposer en deux étapes:
- La définition de la fonction de tâche.
  - L'objectif de commande est formulé comme la minimisation à tout instant d'une somme pondérée de fonctions de coût scalaires.
  - Chacune des contraintes scalaires correspond à un objectif spécifique à atteindre. Hormis l'objectif principal de suivi de la cible par l'organe terminal du manipulateur mobile, la redondance du système permet d'envisager des objectifs secondaires (évitement des butées articulaires, configuration nominale du bras manipulateur, etc ...).
  - L'ajout d'une dernière fonction de coût, dite de "régularisation", permet d'assurer l'évitement de singularités possibles de la fonction de tâche. Remarquons que la régularisation est localement définie autour de l'équilibre, c'est pourquoi une phase de planification assure l'annulation initiale de la fonction de tâche.
  - La fonction de tâche est définie comme le gradient de la fonction de coût globale.
- La loi de commande cinématique est ensuite déterminée de sorte à stabiliser exponentiellement la fonction de tâche à zéro.
Cette formulation de la fonction de tâche présente l'avantage d'une certaine souplesse via le choix des objectifs secondaires de commande. Ces choix influent sur la stratégie de coordination entre la base mobile et le bras manipulateur.

Nous avons validé cette approche par des simulations sous MATLAB dans le cas d'une base mobile omnidirectionnelle porteuse d'un bras manipulateur.
Traitement de la non-holonômie.

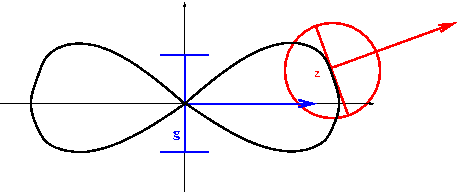
La difficulté à commander les systèmes non-holonômes vient du fait que leurs approximations linéaires en un point d'équilibre ne sont pas stabilisables. L'approche par fonctions transverses (2,3) permet de synthétiser des lois de commande par retour d'état pour la stabilisation de ces systèmes. Ces commandes assurent la stabilisation asymptotique, non pas du point d'équilibre du système, mais d'un ensemble contenu dans un "petit" voisinage borné de ce point (voir Fig. 1).

Plus précisément, pour un système non-holonôme du type 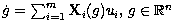$\dot{g}=\sum_{i=1}^m \mathbf{X}_i(g) u_i, \; g \in \mathbb{R}^n$ avec 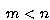, l'approche par fonctions transverses fait intervenir une fonction 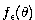$f_\epsilon(\theta)$ périodique dont la variation infinitésimale est "transverse" aux directions données par les champs de vecteurs 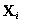évalués en 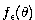$f_\epsilon(\theta)$ . Cette fonction est d'autre part associée à un changement de variables 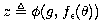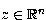$z \triangleq \phi(g,\; f_\epsilon(\theta))$ , $z \in \mathbb{R}^n$ tel que 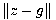et 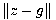sont toujours proches l'un de l'autre, et tel que, le long des trajectoires du système, l'équation de variation de 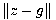est de la forme 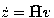$\dot{z}=\mathbf{\bar{H}} v$ , avec $\mathbf{\bar{H}}$ inversible et le vecteur de commande augmenté $v = [u_1 \cdots u_m \dot{\theta}]^t$ . Cette équation, similaire à celle d'un système holonôme complétement commandé, permet de controler la variable 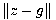plus simplement que l'état 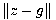du système de départ.

Fig. 1. Unicycle en bleu, son approximation holonôme en rouge et la projection dans le plan de l'ensemble stabilisé en noir.

Une application possible de ce type d'approche est la stabilisation pratique d'un système non-holonôme le long d'une trajectoire de référence quelconque. Des validations de cette méthode ont été réalisées en simulation sous MATLAB et expérimentalement sur le robot mobile ANIS du projet, dans le cadre du suivi référencé vision d'une cible omnidirectionnelle par un véhicule de type unicycle (4).
Commande du manipulateur mobile via la définition d'un système omnidirectionnel transverse équivalent.

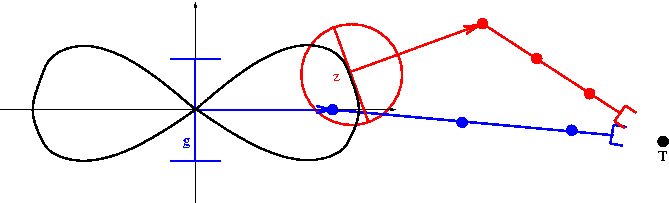
Le principe est de coupler les deux approches précédemment décrites. La synthèse de commandes assurant le suivi de la cible omnidirectionnelle T par l'organe terminal du bras se compose des trois étapes suivantes:
- La définition d'un système omnidirectionnel transverse équivalent au système non-holonôme par rapport à la tâche de suivi. Le système omnidirectionnel transverse équivalent est obtenu par un changement de variables utilisant l'approche par fonctions transverses (§2) et la compensation, au niveau de l'organe terminal, de l'erreur en position de la base non-holonôme, grâce aux degrés de liberté apportés par le bras (voir Fig. 2).
  
  Fig. 2. Système non-holonôme en bleu et son système omnidirectionnel transverse équivalent en rouge.
- La construction d'une fonction de tâche associée au système omnidirectionnel transverse équivalent, assimilable au système holonôme précédemment étudié (§1), et l'élaboration d'une loi de commande cinématique pour ce système assurant la stabilisation des composantes de la fonction de tâche à zéro.
- La loi de commande cinématique du système non-holonôme en est alors déduite grâce au changement de variables entre les deux systèmes.
Ces commandes ont été validées par des simulations sous MATLAB dans le cas d'une base mobile de type unicycle porteuse d'un bras manipulateur. La suite de ce travail portera sur:
- L'implémentation et la validation de ces lois de commande sur le dispositif expérimental ANIS.
- La généralisation de cette approche à des architectures robotiques différentes (robots mobiles à bases non-holonômes de type voiture, par exemple), et pour la réalisation d'autres tâches.