


suivant: Méthodes de filtrage local
monter: Contraintes globales
précédent: Contraintes globales
Table des matières
La contrainte all-diff
La contrainte all-diff traite un
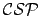 , ou un sous-problème d'un
, ou un sous-problème d'un
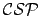 , ayant un certain
nombre de variables dont les valeurs potentielles varient dans des domaines finis, et
contraintes à être toutes différentes.
Autrement dit,
, ayant un certain
nombre de variables dont les valeurs potentielles varient dans des domaines finis, et
contraintes à être toutes différentes.
Autrement dit,
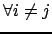 tels que
tels que
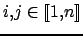 , on a
, on a
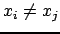 .
Au lieu d'avoir
.
Au lieu d'avoir
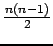 contraintes à traiter, on ne parle
que d'une seule, que l'on nomme la contrainte all-diff.
L'exemple 2.1 est une instance d'un tel
contraintes à traiter, on ne parle
que d'une seule, que l'on nomme la contrainte all-diff.
L'exemple 2.1 est une instance d'un tel
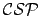 ,
qui illustre parfaitement les difficultés des méthodes basées sur l'arc consistance
pour résoudre ce type de problèmes.
,
qui illustre parfaitement les difficultés des méthodes basées sur l'arc consistance
pour résoudre ce type de problèmes.
Figure 1:
Illustration de la contrainte globale All-diff
|
|
L'algorithme proposé par J.C. Régin [10], modélise les variables et les valeurs des domaines
par un graphe biparti. Puis en quelques étapes il établit l'arc cohérence, de manière à
ce qu'on ne puisse pas trouver un meilleur filtrage(consistance globale).
C'est un algorithme en temps polynômial :
- À partir du
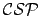 , génerer un graphe biparti variable-valeur.
, génerer un graphe biparti variable-valeur.
- Calculer le couplage maximum du graphe
- Si une variable est libre, alors pas de solutions
- Appliquer la décomposition de Dulmage-Mendelson à partir du couplage obtenu.
- Calculer les composantes fortement connexes de la partie ``bien-valuée''
- Éliminer les valeurs des domaines correspondant aux arètes reliant les parties
``bien-valuée'' et ``sur-valuée'' et aux arètes reliant dux composantes fortement connexes.



suivant: Méthodes de filtrage local
monter: Contraintes globales
précédent: Contraintes globales
Table des matières
Heikel Batnini
2002-10-22
![\includegraphics[scale=0.75]{alldiff.eps}](img96.png)