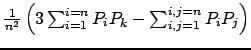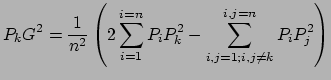


suivant: Trace de la 2B-consistance
monter: Bibliographie
précédent: Démonstration de la propriété
Table des matières
Soit
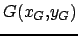 l'isobarycentre de l'ensemble des points
l'isobarycentre de l'ensemble des points
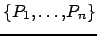 .
.
On a
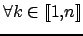 ,
,
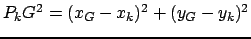 .
.
De plus, d'après la définition 5.1 on a :
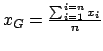 et
et
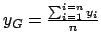
Finalement on peut simplifier l'écriture et
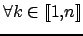 on a :
on a :
 .
.
Heikel Batnini
2002-10-22
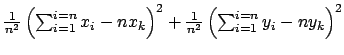
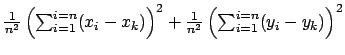
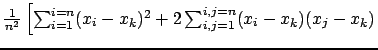
![$ \left. + \sum_{i=1}^{i=n}(y_i - y_k)^2 + 2\sum_{i,j=1}^{i,j=n}(y_i-y_k)(y_j-y_k) \right]$](img344.png)
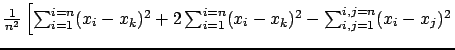
![$ \left. + \sum_{i=1}^{i=n}(y_i - y_k)^2 + 2\sum_{i=1}^{i=n}(y_i - y_k)^2 - \sum_{i,j=1}^{i,j=n}(y_i-y_j)^2 \right]$](img349.png)
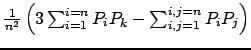
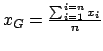 et
et
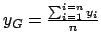
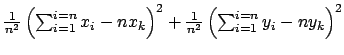
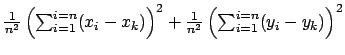
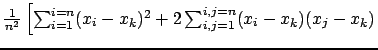
![$ \left. + \sum_{i=1}^{i=n}(y_i - y_k)^2 + 2\sum_{i,j=1}^{i,j=n}(y_i-y_k)(y_j-y_k) \right]$](img344.png)
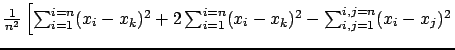
![$ \left. + \sum_{i=1}^{i=n}(y_i - y_k)^2 + 2\sum_{i=1}^{i=n}(y_i - y_k)^2 - \sum_{i,j=1}^{i,j=n}(y_i-y_j)^2 \right]$](img349.png)