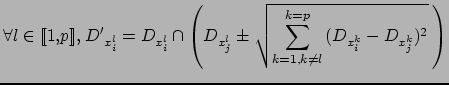Algorithme abstrait :
procedure CLOSE-FILTER(
pour k
pour j
pour i
si
si
sinon si
si
FILTER-DOMAINS(
finpour
finpour
finpour
retourner
La fonction FILTER-DOMAINS(
Notre idée est d'incorporer au traitement d'une arète,
le filtrage des coordonnées de ses extrémités, en projetant simplement chacun des domaines
sur la contrainte liée à cette arête.
L'algorithme ci-dessous réalise cette opération de fermeture en filtrant à la volée les domaines des variables.
L'opération de projection se faisant en temps linéaire de la dimension de l'espace de travail, ![]() ),
l'algorithme de fermeture-filtrage a une complexité en temps de
),
l'algorithme de fermeture-filtrage a une complexité en temps de
![]() .
.
Algorithme abstrait :
procedure CLOSE-FILTER(
![]() )
)
pour k
![]() 1 à
1 à ![]() faire
faire
pour j
![]() 1 à
1 à ![]() faire
faire
pour i
![]() 1 à
1 à ![]() faire
faire
si
![]() alors
alors
![]()
si
![]() alors
alors
![]()
sinon si
![]() alors
alors
![]()
si
![]() alors Erreur
alors Erreur
FILTER-DOMAINS(![]() )
)
finpour
finpour
finpour
retourner
![]()
La fonction FILTER-DOMAINS(![]() ) utilise la contrainte
) utilise la contrainte ![]() de la forme :
de la forme :
![]() pour les filtrer les domaines
des coordonnées des points
pour les filtrer les domaines
des coordonnées des points ![]() et
et ![]() en faisant une projection des domaines :
en faisant une projection des domaines :