N'imprimez pas cette page directement,
téléchargez plutôt une version imprimable au format pdf

Les champs de vecteurs ou de directions sont des objets couramment utilisés pour la visualisation scientifique. Ils associent un vecteur ou une direction à tout point de l'espace, et caractérisent par exemple la vitesse et la direction d'un fluide ou la force et la direction d'une force magnétique ou gravitationnelle (voir figure ci-dessous).

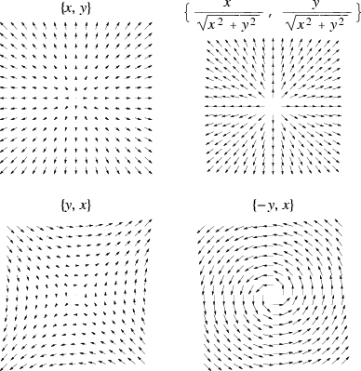
Exemples de champs de vecteurs.

Une manière efficace de visualiser un champ de vecteurs ou de directions consiste à couvrir le domaine étudié par un ensemble de lignes de courant, car elles donnent une bonne information sur la topologie du champs étudié. Une ligne de courant, ou streamline possède en tous points une tangente équivalente au vecteur ou parallèle à la direction. Dans le cas d'un champs de vitesse d'un fluide elle correspond à la trajectoire d'une particule sans masse entraînée par le courant. Si l'écoulement est stationnaire (constant au cours du temps), une particule suit continuellement la même trajectoire, engendrant ainsi la même ligne de courant. Le tracé d'une ligne de courant se fait en général par intégration successive de l'équation de transport du flux par rapport au temps.

Le problème auquel on s'intéresse est celui du placement de lignes de courant (voir figure ci-dessous). Plus précisément, il s'agit d'échantillonner le domaine avec un ensemble de courbes dont la densité est contrôlée. Les longues courbes sont privilégiées aux courtes afin de mettre en évidence la cohérence du flux, et il est souhaitable d'éviter que les régions soient trop denses ou trop vides de lignes de courant.

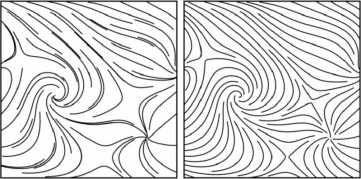
Visualisation d'un champ de vecteurs par un ensemble de lignes de courant. A gauche, l'algorithme procède par initialisation sur une grille régulière. A droite, un meilleur placement.

La majorité des méthodes existantes exploitent la notion de trajectoire de particules germes lâchées dans le flux. Pour chaque germe une ligne de courant est tracée par intégration successive de l'équation de transport du flux jusqu'à être stoppée par des critères de distance aux autres lignes de courant, de sortie du domaine, de trajectoire fermée ou de proximité à une singularité. La difficulté est alors réduite au choix des particules germes et à la définition de critères d'arrêt lors du tracé des lignes de courant. D'autres approches consistent à extraire les singularités et à intégrer leur caractéristique dans l'initialisation des germes (voir figure ci-dessous).

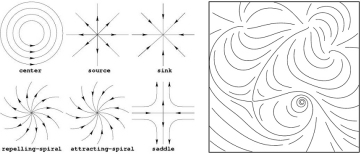
Singularités d'un champ de vecteurs, et placement de lignes de courant
guidé par les singularités.

Bien que de nombreuses solutions aient été proposées à ce problème, une solution variationnelle exprimant les objectifs à atteindre sous la forme d'une énergie à minimiser n'existe pas encore. L'objectif de ce stage consiste à définir cette énergie, puis à en dériver un algorithme d'optimisation afin d'obtenir un placement de lignes de courant en adéquation avec une fonction de densité spécifiée. On s'intéressera notamment au cas des champs de tenseurs 2D, dont les vecteurs propres définissent deux champs de direction orthogonaux.

Outils
PC / linux,
Langage C++,
Bibliothèque de programmes géométriques CGAL

Lieu
INRIA, Unité de Sophia-Antipolis
Projet GEOMETRICA
BP 93 - 06902 Sophia Antipolis, France

Contacts
Pierre Alliez
Tél : 04 92 38 76 77
Olivier Devillers
Tél : 04 92 38 77 63