Direction des Relations et Internationales (DRI)

Programme INRIA "Equipes Associées"

I. DEFINITION

Presentation of the Associate Team

1. Coordinator at the foreign partner

Professor Guibas heads the Geometric Computation group in the Computer Science Department of Stanford University and is a member of the Computer Graphics and Artificial Intelligence Laboratories. He works on algorithms for sensing, modeling, reasoning, rendering, and acting on the physical world. Professor Guibas' interests span computational geometry, geometric modeling, computer graphics, computer vision, sensor networks, robotics, and discrete algorithms --- all areas in which he has published and lectured extensively.
Leonidas J. Guibas obtained his Ph.D. from Stanford University in 1976, under the supervision of Donald Knuth. His main subsequent employers were Xerox PARC, MIT, and DEC/SRC. Since 1984 he has been a professor of Computer Science at Stanford University, where he has developed new courses in algorithms and data structures, geometric modeling, geometric algorithms, and sensor networks. Professor Guibas is an ACM Fellow.

2. History of the collaboration

• 2.1. between teams:
  There is a long history of interactions between the members of both groups. These interactions have become closer and more frequent in the recent years.

  - Back in the 1980's, Jean-Daniel Boissonnat and Leonidas Guibas visited each other's institutions several times. They often met and had technical discussions ever since, at conferences such as STOC, FOCS, SoCG, or SODA.

  - In 1999, Jean-Daniel Boissonnat and Leonidas Guibas participated in the Computational Geometry Impact Task Force Report, Advances in Discrete and Computational Geometry, Contemporary Mathematics, 223, AMS, Providence, RI, pp. 407-463, 1999.

  - In 2005, Jean-Daniel Boissonnat, Leonidas Guibas and Steve Oudot collaborated on the topic of curve and surface probing, where the goal is to learn the shape of an unknown 2- or 3-dimensional object through the interactive process of repeatedly probing its surface. This problem had been considered for some twenty years by the computational geometry community, and solved in the context where the object has a polygonal boundary. Taking advantage of recent advances in curve and surface sampling and reconstruction, Boissonnat, Guibas and Oudot devised a provably-good algorithm for solving the problem in the smooth setting. See J.-D. Boissonnat, L. J. Guibas, S. Y. Oudot, Learning Smooth Objects by Probing, in Proc. 21st ACM Symposium on Computational Geometry, pp. 198-207, 2005. See also J.-D. Boissonnat, L. J. Guibas, S. Y. Oudot, Learning Smooth Shapes by Probing, in Computational Geometry: Theory and Applications, 37:38-58, 2007.

  - After completing his Ph.D. in the Géometrica group at INRIA in Sep. 2005, Steve Oudot was a post-doctoral scholar for two years in the Geometric Computation Group at Stanford University, where he mainly worked with Leonidas Guibas on the topic of multiscale manifold reconstruction --- see below. The main outcomes were: a paper published at SODA'07 (Reconstruction using Witness Complexes, in Proc. 18th Symposium on Discrete Algorithms, pp. 1076-1085), a paper at SoCG'07 in collaboration with Jean-Daniel Boissonnat (Manifold Reconstruction in Arbitrary Dimensions using Witness Complexes, in Proc. 23rd Symposium on Computational Geometry, pp. 194-203), and a paper at SODA'08 in collaboration with Jie Gao and Yue Wang from Stony Brook University (Geodesic Delaunay Triangulation and Witness Complex in the Plane, in Proc. 19th Symposium on Discrete Algorithms). Full versions of these papers are to appear in Discrete and Computational Geometry.

  - In 2006, Daniel Russel, a Ph.D. student of Leonidas Guibas, spent six months as a post-doctoral scholar in the Géometrica group at INRIA, where he collaborated with Monique Teillaud on various topics related to kinetic data structures, including fast and reliable update of the Delaunay triangulation, and reliable computation of arrangements of spheres in 3-space.

  - Steve Oudot is currently collaborating with Leonidas Guibas, as well as Prof. Gunnar Carlsson and his student Gurjeet Singh from the Computational Topology group at the Stanford mathematics department, on an experimental project related to multi-dimensional persistence applied to sensor networks.

• 2.2. between INRIA and the partner institution:

  - To the best of our knowledge, there currently exists only one associate team between INRIA and Stanford University, namely: FS1, founded by the TREC team and the group of Prof. Nick Bambos (electrical engineering department), which focuses on the analysis and design of next-generation wireless networks.

  - There are also three other collaborations, funded in part by the France-Stanford center for interdisciplinary studies:

  • one between the ABS team and the group of Prof. Michael Levitt (biocomputation department), whose goal is to devise new methods for protein folding and protein-protein docking using tools from computational geometry;
  • one between the DEMAR team and the group of Prof. Oussama Khatib (AI laboratory), focused on artificial walking;
  • one between the REO team and the group of Prof. Charles A. Taylor (biomechanical engineering laboratory), whose aim is to use computational simulation to help understand and predict post-intervention hemodynamics for congenital interventions.

  - See the DREI website for the USA.

3. Impact : To what extend do you think this collaboration would have an impact:

II. PREVISIONS 2008

Research Project

The wide availability of scanning technologies for 3-d shape acquisition has led to the development of algorithms and software, in both academia and industry, for building curve or surface meshes from the raw data returned by a scanner --- a problem known as reconstruction. For most optical and contact sensors this raw data is in the form of an unorganized point cloud; current scanners are able to generate surface samplings at submillimeter accuracy. At such high resolutions, fitting a mesh or surface is a well-posed problem, and it is quite naturally that a number of techniques have emerged in the last decade or so to solve the problem both reliably and efficiently. See for instance [3] for a survey of the methods developped by the computational geometry community.

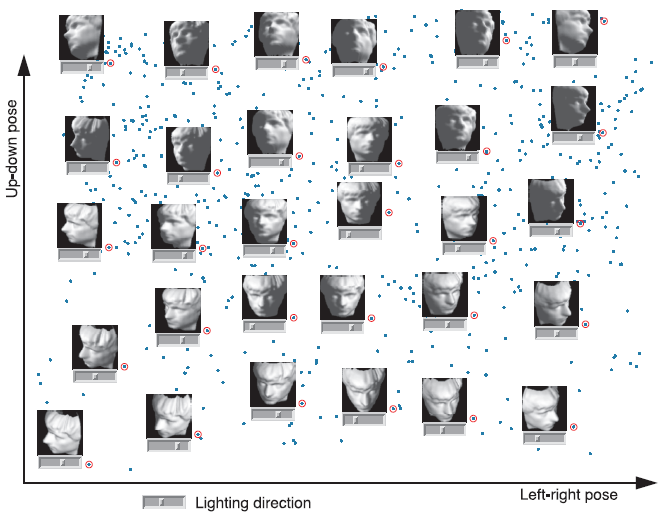
In contrast, high-dimensional data sets usually suffer from significant defects, including under-sampling, noise, and outliers. These defects can be deadly for the reconstruction, and to put things in a few words, reconstructing a manifold from a point cloud with such defects becomes an ill-posed problem, as many different manifolds with diverse geometric and topological features may fit as well to the input data. Furthermore, the high dimensionality of the point cloud makes it impossible to use standard tools from computational geometry, such as Delaunay triangulations, whose complexities grow exponentially with the dimension of the ambient space. This is all the more a pity as the intrinsic dimension of the space underlying the data can be very small. For instance, in the data set of Figure 1 (left), the points represent 64x64-pixels grey-scaled pictures of a same face in various positions and illuminated from various directions: the point cloud is thus 4096-dimensional, whereas the intrinsic dimension of the underlying manifold is only 3: two parameters for the viewing angle, one parameter for the lighting direction. It follows from the above discussion that there is a real need for novel data anlysis techniques that can handle defects in the input reliably, and whose complexities scale up with the intrinsic dimension of the data.

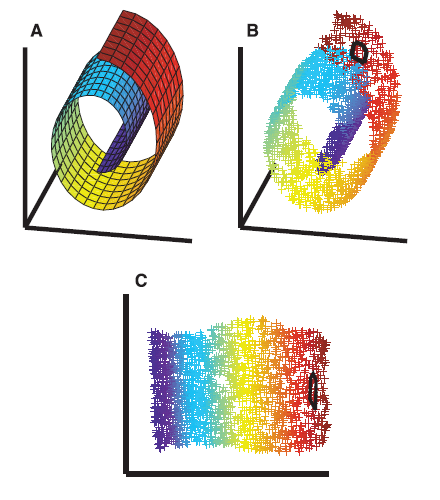
Figure 1: Left: a high-dimensional data set after dimensionality reduction (from [16]). Right: A highly non-linear data set (from [15]).

Previous work

Dimensionality reduction is certainly one of the most popular approaches to high-dimensional data analysis. It consists in projecting the data points down to a linear subspace, whose dimension supposedly coincides with the intrinsic dimension of the data. This approach is elegant in that it helps detect the intrinsic parameters of the data, and by doing so it also reduces the complexity of the problem. For instance, on the data set introduced above, the approach ideally reduces the dimension from 4096 down to 3, thereby exhibiting the 3 degrees of freedom of the original setup. Dimensionality reduction techniques fall into two classes: linear methods, e.g. principal component analysis (PCA) or multi-dimensional scaling (MDS), and non-linear methods, e.g. isomap or locally-linear embedding (LLE). The second class of algorithms is more powerful in that it computes more general (in fact, non-linear) projections. For instance, isomap and LLE can flatten the data set of Figure 1 (right), while preserving locality relationships between the data points, which linear techniques such as PCA or MDS cannot. On the whole, dimensionality reduction works well on data sets sampled from manifolds with low curvature and trivial topology. Although the condition on the curvature is mainly a sampling issue, the condition on the topology is mandatory for the projection onto a linear subspace to make sense.

Topological persistence was recently introduced as a powerful tool for the study of the topological invariants of sampled spaces. Given a point cloud in Euclidean space, the approach consists in building a simplicial complex whose elements are filtered by some user-defined function. This filter basically gives an order of insertion of the simplices in the complex. The persistence algorithm, first introduced by Edelsbrunner, Letscher and Zomorodian [11], is able to track down the topological invariants of the filtered complex as the latter is being built. As independently proved by Cohen-Steiner et al. [7] and by Chazal and Lieutier [5], under reasonable conditions on the input point cloud, and modulo a right choice of filter, the most persistent invariants in the filtration correspond to invariants of the space underlying the data. Thus, the information extracted by the persistence algorithm is global, as opposed to the locality relationships used by the dimensionality reduction techniques. In this respect, topological persistence appears as a complementary tool to dimensionality reduction. In particular, it enables to determine whether the input data is sampled from a manifold with trivial topology, a mandatory condition for dimensionality reduction to work properly. Note however that it does not tell how and where to cut the data to remove unwanted topological features. Since its first introduction, topological persistence has been extended in several ways, including multi-dimensional persistence [2], where two or more different functions can be used to filter a same complex, and zig-zag persistence [10], where more general relationships are allowed between the complexes of a filtration. In all cases, the information retrieved using the approach is purely global and topological.

Multiscale reconstruction is a novel approach, independently developped by the Géometrica group at INRIA [4] and the Geometric Computation group at Stanford University [13]. Taking advantage of the ideas of persistence, the approach consists in building a one-parameter family of simplicial complexes approximating the input at various scales. Differently from above, the family may not necessarily form a filtration, but it has other nice properties. In particular, for a sufficiently dense input data set, the family contains a long sequence of complexes that approximate the underlying space provably well, both in a topological and in a geometric sense. In fact, there can be several such sequences, each one corresponding to a plausible reconstruction at a certain scale. 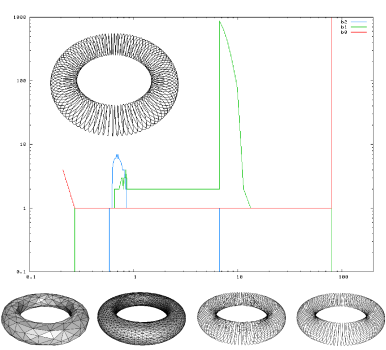Thus, determining the topology and shape of the original object reduces to finding the stable sequences in the one-parameter family of complexes. In the example of Figure 2 (left), the point cloud was sampled from a helical curve drawn on a torus. From this data set, the algorithm of [13] generated a 1-parameter family of complexes (bottom) and maintained their Betti numbers (diagram). The two plausible reconstruction (curve and torus) appear as long plateaus in the diagram.
In [4,6], the family of complexes is derived from the so-called alpha-offsets of the input point cloud, defined as the unions of balls of same radius alpha centered at the data points. In [1,13], the family is derived from the so-called witness complex, first introduced by de Silva [9], which can be viewed as a weak version of the Delaunay triangulation whose construction requires much less computation power. Despite this nice feature, multiscale reconstruction, at least in its current form, still has a complexity that scales up exponentially with the dimension of the ambient space. Hence, it can only be applied to low-dimensional data sets in practice.

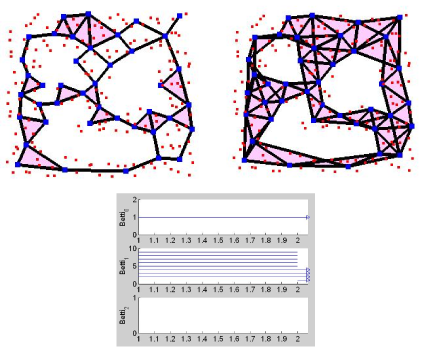
Figure 2: Left: original object (top-left), output family of complexes (bottom) and diagram of Betti numbers (from [13]). Right: WC (left) and EWC (right) sandwich the geodesic Delaunay triangulation (from [12]).

Program for 2008

The sandwich approach. Whenever the data points lie on or close to a Riemannian manifold (M), the witness complex (WC) acts as a weak version of the Delaunay triangulation (Del) in the Riemannian metric. Indeed, as proved recently by de Silva [8], WC is included in Del, which, according to Leibon and Letscher [14], is homeomorphic to M and close to it geometrically, provided that the data set is sufficiently densely sampled on M. In practice, Del is impossible to construct explicitly, because M is unknown. In contrast, WC can be built explicitly, and furthermore in a time that is linear in the input and polynomial in the intrinsic dimension of M. However, WC only provides an approximation by default to the ideal reconstruction Del. In [13], Guibas and Oudot showed how an extended witness complex EWC can be built out of WC, such that Del is sandwiched between WC and EWC. Neither WC nor EWC may have the same topological invariants as M, but Del (which is unknown) does. The claim is that the topological invariants that persist from WC to EWC should coincide with the invariants of Del --- and hence of M. This assertion, illustrated in Figure 2 (right), was proved correct by Guibas, Oudot and others for planar domains [12]. We will try to extend the analysis to higher-dimensional manifolds.

The witness complex filtration. The construction of the extended witness complex EWC is parameterized by a coefficient r that indicates how much to extend the witness complex WC. When r=0, EWC coincides with WC. When r is infinite, EWC coincides with the complete simplex, i.e. the simplex built on top of the complete graph over the data points. By varying r from zero to infinity, one gets a nested 1-parameter family of complexes, the first element of which is WC, and the last element the complete simplex. By applying the persistence algorithm to this filtration, one can detect its most persistent homological features. We claim that, not only do these persistent features correspond to topological invariants of the underlying manifold M, but they also appear very early in the filtration, and at approximately the same time. This assertion, if true, will have two major consequences:

• First, it will not be necessary to build the whole filtration, but only its initial part. This is likely to significantly reduce the size of the data structure, hopefully down to a quantity that will depend solely on the intrinsic dimension of M.
• Second, some of the complexes in the filtration will have the same topological invariants as the manifold M. Hence, by detecting the most persistent topological features in the filtration, we will also detect good candidates for reconstruction among the complexes of the family.

The theory of distance functions. The structural properties that have been associated with the witness complex so far hold only in a rather limited setting, where the data are sampled from smooth manifolds. What if the underlying space is not smooth, or even not a manifold? What if there is noise in the sampling process? In [4], Chazal, Cohen-Steiner and Lieutier introduced the concept of critical function of a compact set, which is derived from the distance to the set. Without giving out too much of the details, this concept enabled them to devise new sampling conditions for point sets drawn from non-smooth or non-manifold spaces, possibly with noise. Using tools from non-smooth analysis, they proved that data sets satisfying such conditions provide a lot of information about their underlying space. In particular, for a wide range of values of alpha, their alpha-offsets carry the same topological type as the space itself and are close to it geometrically. This makes the framework of [4] quite interesting in the context of multiscale reconstruction, even though the size of the alpha-offsets can be exponential in the dimension of the ambient space. Taking advantage of both worlds, we would like to combine the approach based on the witness complex with the framework of distance functions. The outcome would be a theoretical analysis of the structural properties of the witness complex in the extended setting of data sets sampled from non-smooth, non-manifold spaces, possibly with noise. This would greatly increase the impact and practicality of our methods.

Longer term

• Are there data structures, other than the witness complex and its extensions, that approximate the geodesic Delaunay triangulation well, and that are not too costly to compute? Such data structures would certainly lead to new algorithms from the multiscale reconstruction family, and thereby enrich the range of available tools for the analysis of high-dimensional data.
• What is the hardness of the reconstruction problem in arbitrary dimensions? Is it possible to devise a manifold reconstruction algorithm of fully polynomial complexity, that is, whose complexity would be polynomial both in the size of the input point set and in the dimension of the ambient space? Such an algorithm would be able to deal with data sets sampled from high-dimensional manifolds, in particular hypersurfaces, which play an important role in robotics, sensor networks, and related areas.
• Is it possible to extend the sampling theory beyond the class of non-smooth shapes introduced in [4]? In particular, can we reconstruct stratified manifolds with guarantees? A student started a Ph.D. in the Géometrica group this year, on the detection of singularities in point cloud data. His work could possibly be adapted to detect and reconstruct strata in data sets sampled from stratified manifolds. Also, can we perform reconstructions in non-Euclidean spaces, such as parameter spaces for probability distributions? This would be useful in the context of statistical analysis.

Applications. We are also interested in the potential impact of our research on other scientific fields, including (but not restricted to) machine learning, statistics, structural biology, and sensor networks. This is why a lot of effort will be devoted to developing new applications of our techniques in these fields. This will provide us with opportunities to collaborate with other groups, both at INRIA and at Stanford University. On the INRIA side, the Géometrica group is already working together with the ABS team on the application of geometric concepts to structural biology, and with the LEAR team and the group of Prof. Frank Nielsen (through the GAIA project) on topics related to reconstruction in parameter spaces, with applications in statistical analysis. On the Stanford side, the Geometric Computation group has developped long-lasting collaborations on similar topics with the biocomputation lab, the AI lab, and the statistics department.

Experimental validation. Our methods will be consistently set against real-life data sets coming from the various fields of application mentioned above. Through its collaboration with the Geometric Computation group, the Géometrica team will be granted access to the data base of the TDA project, an important resource for practical experimentation. In addition, to make our methods available to the greater number, and eventually get valuable feedback, we plan to integrate them to the C++ library CGAL (Computational Geometry Algorithms Library), and to develop front-ends for benchmark scientific computing software, such as Matlab, Scilab, or Maple. Details are to be discussed between the partners as one goes along.

Bibliography

Planned Budget for 2008

1. Complementary funding

- Does this collaboration already benefit from a financial support from INRIA, or the foreign institute, or any other funding agency (EU project, NSF...)?

The Geometric Computation group will provide funding for our collaboration in 2008, through NSF grant ITR-0205671: Representations and Algorithms for Deformable Objects. This financial support will cover Steve Oudot's visit to Stanford, as well as part of the visit of a Ph.D. student from INRIA.

Both partners are willing to provide financial support for the collaboration. In addition to the existing support, we will apply for a France-Stanford grant in 2008, which, if accepted, will take effect in September 2008 and provide support for short-term visits of INRIA researchers to Stanford University.

Note: the total amount of the France-Stanford grant lies around 10 kE, however the grant is to be used between Sep. 2008 ad Sep. 2009. This is why only about one third of the total amount will be allocated to the 2008 budget.

2. Exchanges

As project coordinator and former post-doctoral intern, Steve Oudot will make a long term visit (several months) to Stanford University. This will ensure continuity between his past collaborations with the groups of Leonidas Guibas and Gunnar Carlsson, and new collaborations between teams on the research topics mentioned in the program. He will bring a fresh Ph.D. student from the Géometrica group along with him, to strengthen the collaboration at junior level, and on the longer term.

Symmetrically, Leonidas Guibas will make a short term visit (1 to 3 weeks) to INRIA, probably around March 2008. In addition, one or two Ph.D. students from the Geometric Computation group will come to INRIA for a total duration of 6 months.

In order to carry out joint research, several other senior researchers from both teams will be involved in the project. Frédéric Chazal, Jean-Daniel Boissonnat and David Cohen-Steiner, from Géometrica, plan short stays (1 to 3 weeks) at Stanford University. Symmetrically, Gunnar Carlsson from the mathematics department at Stanford may be invited for a short stay at INRIA at some point.

We also plan to hire interns at master level to assist us on complementary algorithm components or implementations. However, due to the high complexity of the theoretical questions raised by our research project, we expect this part of the program to be deferred to 2009. We plan to organize a common workshop at that stage.