![\[ 4.30232 e^{- 16}, - 4.99422, 4.99422 \]](form_536.png)
Suppose for instance that we are manipulating univariate polynomials with integer coefficients (ZZ) and that we want to compute the real roots by the Aberth method. Then after including the file:
#include <synaps/usolve/Aberth.h>
we can use the instruction:
We obtain
![\[ 4.30232 e^{- 16}, - 4.99422, 4.99422 \]](form_536.png)
Instead, if we use Aberth<CC>(), we obtain the sequence of all the 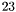 complex roots. Notice that these are approximate values of the actual roots. The way to decide wether we have a real or a complex roots depends on a threshold. The level of approximation is controled by the class Aberth.
complex roots. Notice that these are approximate values of the actual roots. The way to decide wether we have a real or a complex roots depends on a threshold. The level of approximation is controled by the class Aberth.
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include <synaps/arithm/gmp.h> #include <synaps/upol/UPolDse.h> #include <synaps/usolve/Aberth.h> int main(int argc, char** argv) { using std::cout; using std::endl; UPolDse<QQ> p("x^7-2324325131254354*x-1"); cout<<p<<endl; Seq<RR> sol= solve(p, SlvAberth<RR>()); cout<<sol<<endl; cout<<p(sol[1])<<endl; } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
Exercise: Compute the real (resp. complexe) roots of the polynomial ![$W_n (x) = \prod_1^n (x - i) \in \mathbbm{Q}[x]$](form_520.png) for n=20. Same question for for n=20. Same question for 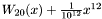 . .  |
If one is intereseted in the root of polynomial in an interval, subdivision solvers may be used. The following solver is using the Bernstein basis representation in order to approximate or isolate the real roots of a polynomial. It requires the following files:
#include <synaps/usolve/bezier/SlvBzStd.h> #include <synaps/usolve/bezier/SlvBzBdg.h> #include <synaps/usolve/bezier/IslBzStd.h>
UpolDse<ZZ> p("x^7-2324325131254354*x-1");
cout<< solve(p, SlvBzStd<double>(1e-6)) << endl;
cout<< solve(p, SlvBzBdg<double>(1e-6), -400., 500.) << endl;
![$[- 400, 500]$](form_539.png) . The two solvers yields different approximation of the roots:
. The two solvers yields different approximation of the roots:
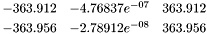
cout<< solve(p, IslBzStd<QQ>(1e-6)) << endl;
 such that
such that ![$[a_i, b_i]$](form_542.png) contains only one root of p:
contains only one root of p:
![\[ - 2324325131254355, - 1, - 1, 0, 1, 2324325131254355 \]](form_543.png)
The naming convention, which we use is the following: Slv... is solver which approximate the real roots, Isl... is a solver which isolate the real roots.
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include <synaps/arithm/gmp.h> #include <synaps/upol/UPolDse.h> #include <synaps/usolve/bezier/SlvBzStd.h> #include <synaps/usolve/bezier/SlvBzBdg.h> #include <synaps/usolve/bezier/IslBzStd.h> int main(int argc, char** argv) { using std::cout; using std::endl; UPolDse<ZZ> p("x^7-2324325131254354*x-1"); cout<<p<<endl; cout<<solve(p, SlvBzStd<double,double>())<<endl; cout<<solve(p, SlvBzBdg<double,QQ>(), -400., 500.)<<endl; cout<<solve(p, IslBzStd<QQ,QQ>())<<endl; } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
Roots of polynomials over 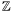 can be manipulated exactly, as algebraic numbers. Their internal representation will be the defining polynomial and an interval of isolation. It requires the following file:
can be manipulated exactly, as algebraic numbers. Their internal representation will be the defining polynomial and an interval of isolation. It requires the following file:
#include <synaps/usolve/Algebraic.h>
UpolDse<ZZ> p("x^7-2314*x-1"),q("x^3-2*x+1"); typedef algebraic::real<QQ> algebraic_t; Seq<algebraic_t> sol= solve(p, Algebraic<QQ>()); cout<<SignAt(q,sol[0])<<endl;
![\begin{eqnarray*} \tmop{root}_\tmop{of} (x^7 - 2324325131254354) x - 1, 1) \tmop{in} & [- \frac{2324325131254355}{439804651104}, \frac{- 2324325131254355}{8796093022208}], & \tmop{approx} = - 363.956,,\\ \tmop{root}_\tmop{of} (x^7 - 2324325131254354 x - 1, 1) \tmop{in} & [0, 2324325131254355], & \tmop{approx} = 363.956,\\ \tmop{root}_\tmop{of} (x^7 - 2324325131254354) x - 1, 1) \tmop{in} & [ \frac{- 2324325131254355}{8796093022208}, 0], & \tmop{approx} = - 3.00412 e^{- 11} \end{eqnarray*}](form_545.png)
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include <synaps/arithm/gmp.h> #include <synaps/upol/UPolDse.h> #include <synaps/usolve/algebraic/sign_fct.h> #include <synaps/usolve/Sturm.h> typedef ALGEBRAIC::root_of<ZZ> algebraic_t; int main(int argc, char** argv) { using std::cout; using std::endl; UPolDse<ZZ> p("x^7-2324325131254354*x-1"), q("x^3-2*x-1"); cout<<p<<endl; Seq<algebraic_t> sol = solve(p, Sturm<ZZ>()); cout<<sol<<endl; cout<<sign_at(p,sol[1])<<","<<sign_at(q,sol[1])<<endl; } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
#include <synaps/msolve/Newmac.h>
typedef MPol<RR> mpol_t; std::list<mpol_t> E; E.push_back(mpol_t("x^2+y^2+z^2-1")); E.push_back(mpol_t("x^2+2*x*y-y^2+z^2-1")); E.push_back(mpol_t("3*x^2-x*y+4*y^2+z^2-2*x-3*y+z-2")); Seq<VectDse<std:complex<long double> > > sol = solve(E, Newmac<RR>()); cout<< sol <<endl;
![\begin{eqnarray*} {}[ & (1.40281, 0.277651), (1.40281, 0.277651), (0.450884, - 1.72768) & ],\\ {}[ & (1.40281, - 0.277651), (1.40281, - 0.277651), (0.450884, 1.72768) & ],\\ {}[ & (- 0.305627, - 1.35784 e^{- 17}), (- 0.30 b 5627, - 2.26906 e^{- 17}), (- 0.901767, - 4.39707 e^{- 17}) & ],\\ {}[ & (- 0.576379, - 1.25406 e^{- 17}), (- 1.62598 e^{- 16}, 2.08405 e^{- 17}), (- 0.817183, - 2.11964 e^{- 17}) & ],\\ {}[ & (1.28819, - 0.274842), (9.78732 e^{- 17}, 3.27854 e^{- 16}), (0.408591, 0.866511) & ],\\ {}[ & (1.28819, 0.274842), (2.14442 e^{- 16}, - 6.61071 e^{- 17}), (0.408591, - 0.866511) & ],\\ {}[ & (1.40634 e^{- 09}, 1.43066 e^{- 08}), (- 9.37557 e^{- 10}, - 9.53772 e^{- 09}), (1, 2.382 e^{- 15}) & ],\\ {}[ & (- 1.40634^{- 09}, - 1.43066 e^{- 08}), (9.37557 e^{- 10}, 9.53772 e^{- 09}), (1, - 7.4936 e^{- 16}) & ] \end{eqnarray*}](form_546.png)
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include <synaps/arithm/gmp.h> #include <synaps/mpol.h> #include <synaps/msolve/Newmac.h> typedef MPol<double> mpol_t; int main(int argc, char** argv) { using std::cout; using std::endl; std::list<mpol_t> E; E.push_back(mpol_t("x^2+y^2+z^2-1")); E.push_back(mpol_t("x^2+2*x*y-y^2+z^2-1")); E.push_back(mpol_t("3*x^2-x*y+4*y^2+z^2-2*x-3*y+z-2")); cout<<solve(E,Newmac<double>())<<endl; // [(1.40281,0.277651),(1.40281,0.277651),(0.450884,-1.72768)], // [(1.40281,-0.277651),(1.40281,-0.277651),(0.450884,1.72768)], // [(-0.305627,-1.35784e-17),(-0.305627,-2.26906e-17),(-0.901767,-4.39707e-17)], // [(-0.576379,-1.25406e-17),(-1.62598e-16,2.08405e-17),(-0.817183,-2.11964e-17)], // [(1.28819,-0.274842),(9.78732e-17,3.27854e-16),(0.408591,0.866511)], // [(1.28819,0.274842),(2.14442e-16,-6.61071e-17),(0.408591,-0.866511)] // [(1.40634e-09,1.43066e-08),(-9.37557e-10,-9.53772e-09),(1,2.382e-15)], // [(-1.40634e-09,-1.43066e-08),(9.37557e-10,9.53772e-09),(1,-7.4936e-16)], } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
The subdivision solver can be used from the file
#include <synaps/msolve/sbdslv.h>
We define the domain ![$[a_1, b_1] \times \cdots \times [a_n, b_n]$](form_547.png) where we search the roots by the vector:
where we search the roots by the vector:
VectDse<double> domain(6,"-1 1.1 -1 1.1 -1 1.1");
cout<<solve(E, SBDSLV<double,SBDSLV_RDRDL>(1e-6), domain)<<endl;
![\begin{eqnarray*} {}[ & 5.72114 e^{- 08} 4.53431 e^{- 08} 1 & ]\\ {}[ & - 0.576379 - 2.21964 e^{- 10} - 0.817183 & ]\\ {}[ & - 0.305627 - 0.305627 - 0.901767 & ] \end{eqnarray*}](form_548.png)
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include <synaps/arithm/gmp.h> #include <synaps/mpol.h> #include <synaps/msolve/Newmac.h> typedef MPol<double> mpol_t; int main(int argc, char** argv) { using std::cout; using std::endl; std::list<mpol_t> E; E.push_back(mpol_t("x^2+y^2+z^2-1")); E.push_back(mpol_t("x^2+2*x*y-y^2+z^2-1")); E.push_back(mpol_t("3*x^2-x*y+4*y^2+z^2-2*x-3*y+z-2")); cout<<solve(E,Newmac<double>())<<endl; // [(1.40281,0.277651),(1.40281,0.277651),(0.450884,-1.72768)], // [(1.40281,-0.277651),(1.40281,-0.277651),(0.450884,1.72768)], // [(-0.305627,-1.35784e-17),(-0.305627,-2.26906e-17),(-0.901767,-4.39707e-17)], // [(-0.576379,-1.25406e-17),(-1.62598e-16,2.08405e-17),(-0.817183,-2.11964e-17)], // [(1.28819,-0.274842),(9.78732e-17,3.27854e-16),(0.408591,0.866511)], // [(1.28819,0.274842),(2.14442e-16,-6.61071e-17),(0.408591,-0.866511)] // [(1.40634e-09,1.43066e-08),(-9.37557e-10,-9.53772e-09),(1,2.382e-15)], // [(-1.40634e-09,-1.43066e-08),(9.37557e-10,9.53772e-09),(1,-7.4936e-16)], } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
 |