![\[ f (x, y) = \sum_{0 \leqslant i \leqslant d_1, 0 \leqslant j \leqslant d_2} c_{i, j} B^i_{d_1} (x ; a, b) B^j_{d_2} (y ; c, d), \]](form_470.png)
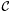 , defined by an implicit equation
, defined by an implicit equation 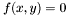 , where
, where ![$f \in \mathbbm{Q}[x, y]$](form_468.png) . It uses the representation of polynomials in the Bernstein basis of a domain
. It uses the representation of polynomials in the Bernstein basis of a domain ![$[a, b] \times [c, d]$](form_469.png) :
:
![\[ f (x, y) = \sum_{0 \leqslant i \leqslant d_1, 0 \leqslant j \leqslant d_2} c_{i, j} B^i_{d_1} (x ; a, b) B^j_{d_2} (y ; c, d), \]](form_470.png)
where 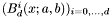 is the Bernstein basis in degree
is the Bernstein basis in degree 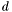 , on the interval
, on the interval ![$[a, b]$](form_183.png) . The polynomial
. The polynomial 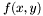 will be represented by its control coefficients
will be represented by its control coefficients 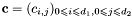 and the domain
and the domain ![$[a, b] \times [c, d]$](form_469.png) . It can be subdivided by applying the de Casteljau algorithm, in the
. It can be subdivided by applying the de Casteljau algorithm, in the 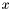 and
and 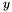 direction.
direction.
The subdivision algorithm is based on a criterion for detecting the regularity of the curve 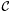 , in the domain
, in the domain ![$[a, b] \times [c, d]$](form_469.png) .
.
Definition: We say that a domain ![$D = [a, b] \times [c, d]$](form_474.png) is regular for is regular for 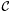 , if its topology in , if its topology in 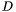 is uniquely determined from the intersection points of is uniquely determined from the intersection points of 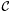 , with the boundary , with the boundary 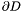 of of 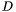 . . |
Here is a property that we use to detect regular domains:
Proposition: If 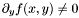 (resp. (resp. 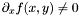 ) in ) in ![$D = [a, b] \times [c, d]$](form_474.png) , then , then 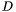 is regular for is regular for 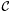 . . |
The test is implemented by checking that the control coefficients of 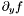 or
or 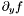 on D have a constant sign, which implies the previous proposition.
on D have a constant sign, which implies the previous proposition.
|
Algorithm: Subdivision algorithm for implicit curves.
input:
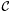 . . |
void topology::assign(point_graph<C> & g, MPol<QQ>& p, TopSbdBdg2d<C> mth, C x0, C x1, C y0, C y1);
g of type topology::point_graph<C>, which is isotopic to the curve defined by the polynomial p, in the box ![$B = [x_0, x_1] \times [y_0, y_1]$](form_485.png) . The coordinates of the points in
. The coordinates of the points in g are of type C. The implementation is designed for C=double.p are rational numbers. During the computation, they are rounded to double number types. If the topology in the box can be certified from this approximation, a graph of points connecting the intersection of the curve with the boundary of 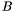 is computed. Otherwise the box is subdivided into
is computed. Otherwise the box is subdivided into 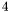 subboxes and the test is applied recursively.
subboxes and the test is applied recursively.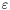 specified by the class
specified by the class TopSbdBdg2d<C>. The default value is 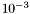 .
.synaps/topology/TopSbdBdg2d.h, TopSbdBdg.![]()
![]()
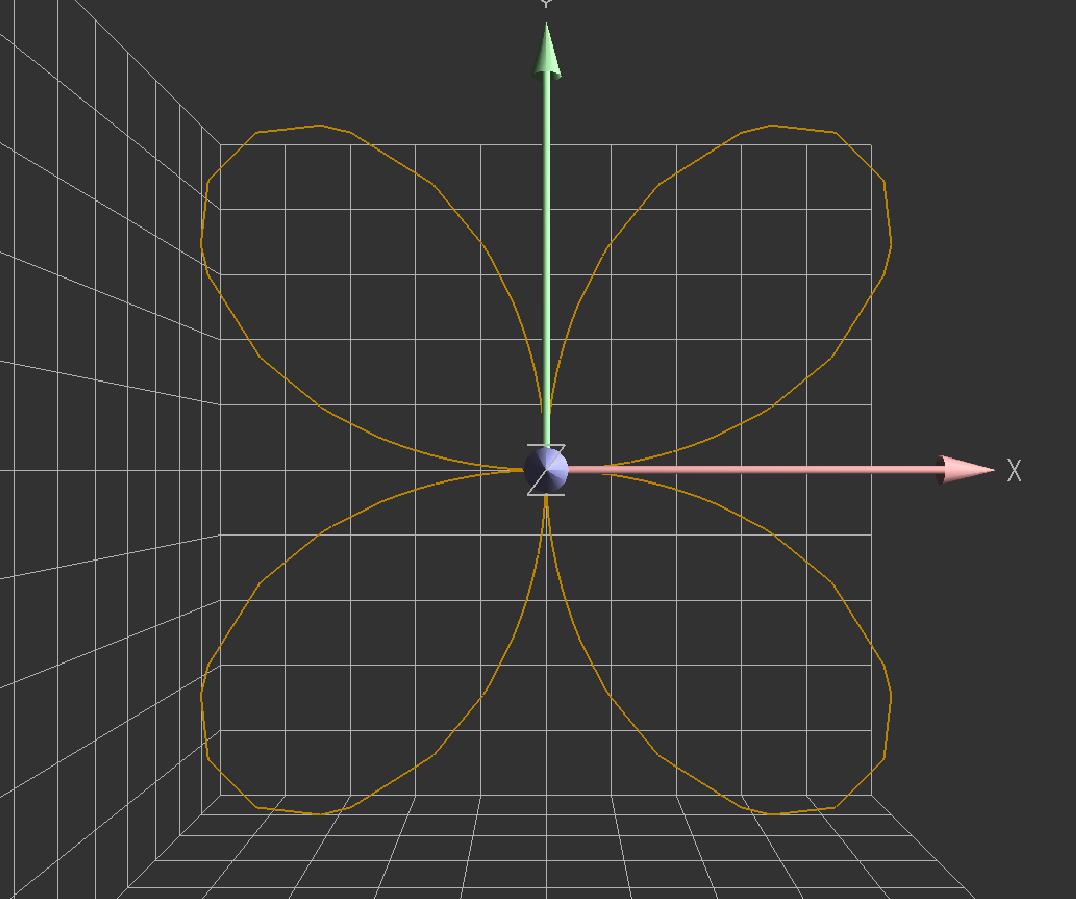
#include <synaps/topology/TopSbdBdg2d.h> int main(int argc, char** argv) { MPol<QQ> p("x^6+3*x^4*y^2+3*x^2*y^4+y^6-4x^2*y^2"); topology::point_graph<double> g; topology::assign(g, p, TopSbdBdg2d<double>(), -2., 2.1, -2.2, 2., 2); }
Here is a picture of such output:
 |