Univariate Continued Fraction solver |
The family of methods based on continued fraction expansion proceed as follows:
Algorithm solve_continued_fraction(f,
Compute an integer lower
Shift
Compute the number
if
Split the polynomial
Apply reccursively the algorithm on
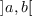 )
)
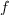 on the interval
on the interval 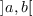 .
.
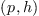 where
where 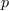 is a
univariate polynomial expressed in the monomial basis
and
is a
univariate polynomial expressed in the monomial basis
and 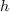 is an homography such that
is an homography such that
 and and
and and 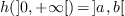 .
.
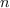 bound
of the positive roots of
bound
of the positive roots of 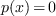 ;
;
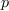 by
by 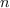 :
:
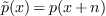 ;
;
 of sign
changes of the coefficients of
of sign
changes of the coefficients of 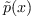 ;
;
 then output the
corresponding isolation interval and stop; if
then output the
corresponding isolation interval and stop; if  stop also;
stop also;
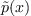 in
in 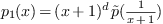 whose positive roots correspond to
the roots of
whose positive roots correspond to
the roots of 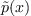 in
in 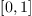 ,
,  whose positive
roots correspond to the roots of
whose positive
roots correspond to the roots of 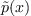 in
in 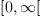 .
.
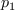 and
and 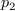 .
.
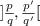 where
where 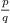 and
and 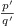 are consecutive continued fraction
approximations of a root
are consecutive continued fraction
approximations of a root  of
of 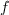 and such that all roots of
and such that all roots of  of
of 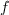 is in one of these intervals.
is in one of these intervals.
Such a solver computes the first terms of the continued fraction expansion of the roots of a univariate polynomial. Two variants are also available, depending wether we want to isolate or approximate the real roots.