 |
The ring of sparse polynomials |
 |
Sparse polynomials are represented as an ordered list of monomials. The corresponding type is Polynomial MonomialSparseRing C, where C is the type of coefficients. Here we describe the main functionnalities available for these polynomials.
Mmx]
use "realroot"
1.Constructors
1.1.Ring constructors
Mmx]
R := ZZ[x,y]
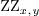
Mmx]
ring (ZZ,'x,'y,'z)
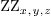
1.2.Polynomial constructors
Construction of a polynomial from variables from the ring:
Mmx]
x:= R[0]; p := 215*x^4+10*x-3232231
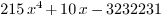
Construction of a polynomial from a string:
Mmx]
p:= R<<"215*x^4+10*x-3232231"
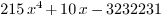
Mmx]
q := polynomial(R,"3*x^3*z-x^2*y+2")
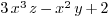
An equivalent construction with variables
Mmx]
y:=R[1], z:= R[2]; q := 3*x^3*z-x^2*y+2
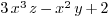
Mmx]
2.Functions
2.1.Aritmetic operations
Arithmetic operations inherited from the coefficient ring are available:
Mmx]
p+33455552
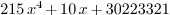
Mmx]
q+=p
Mmx]
r:=q*p
Mmx]
2.2.Coefficients
Coefficients with respect to variable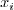 
(the
results is a list of multivariate polynomials):
Mmx]
coefficients(r,0)
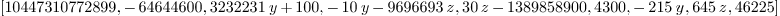
Mmx]
coefficients r
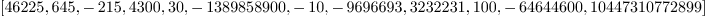
Mmx]
2.3.Differentiation
Mmx]
diff(r,'x)
Mmx]
diff(r,0)
Mmx]
2.4.Homogeneization
Mmx]
homogenize(q,R<<'w)
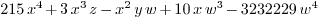
Mmx]