| Modular numbers |
This document describes the use and implementation of the modulars within the numerix package.
1.General modulars and moduli
Moduli are implemented in modulus.hpp. An object of type modulus is declared as follows:
modulus<C,V> p;
V is an implementation variant. The default variant, named modulus_naive, is implemented in modulus_naive.hpp and supports a type C with an Euclidean division. More variants are described below. Modulars are implemented in modular.hpp. An object of type modular can be used as follows:
modular<modulus<C, V>, W> x, y, z;
modular<modulus<C, V>, W>::set_modulus (p);
x = y * z;
The variant W is used to define the storage of the
modulus. Default storage is modular_local
that allows the current modulus to be changed at any time. The default
modulus is 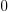 . For the integer
type the default variant is set to modulus_integer_naive,
so that modular integers can be used as follows:
. For the integer
type the default variant is set to modulus_integer_naive,
so that modular integers can be used as follows:
#include<numerix/integer.hpp>
#include<numerix/modular.hpp>
#include<numerix/modulus_integer_naive.hpp>
typedef modulus<integer> M;
M p (9973);
modular<M>::set_modulus (p);
modular<M> a (1), b (3);
c = a * b;
cout << c << "\n";
If the modulus is known to be fixed at compilation time then the following declaration is preferable for the sake of efficiency:
fixed_value <int, 3> w;
modulus<integer> p (w);
If the modulus is not intended to be changed and known at compilation time then the variant modular_fixed can be used.
2.Moduli for hardware integers
From now on 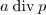 and
and 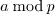 represent the quotient and the remainder in the long division of
represent the quotient and the remainder in the long division of  by
by 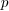 respectively. Throughout
this section C denotes a genuine integer C type. We
write
respectively. Throughout
this section C denotes a genuine integer C type. We
write 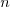 for the bit-size of C,
and
for the bit-size of C,
and 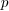 for a modulus that fits in C.
for a modulus that fits in C.
2.1.Naive implementation
The default variant, modulus_int_naive<m>,
is defined in modular_int.hpp. Each
modular product performs one product and one integer division. The
parameter m is the maximum bit-size of the modulus
allowed by the variant. This parameter can be set to 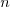 .
Best performances are obtained with m
.
Best performances are obtained with m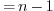 .
Note that we necessarily have m
.
Note that we necessarily have m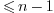 if C is a signed integer type. By convention the
modulus
if C is a signed integer type. By convention the
modulus 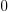 actually means
actually means 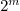 .
.
2.2.Moduli with pre-computed inverse
In the variant modulus_int_preinverse<m>
a suitable inverse of the modulus is pre-computed and stored as an
element of type C, this yields faster computations
when doing several operations with the same modulus. The behavior of
the parameter m is as in the preceding naive variant.
The best performances are attained for when m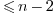 .
.
Within the implementation of this variant the following auxiliary quantities are needed:
-
a non-negative integer
 is defined by
is defined by 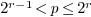 ,
,
-
an integer
 such that
such that 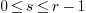 ,
,
-
an integer
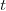 such that
such that  and
and 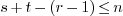 ,
,
-
an integer
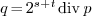 , that represents the numerical
inverse of
, that represents the numerical
inverse of 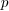 to precision
to precision 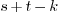 .
.
By convention we let  if
if 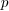 is zero. Note that
is zero. Note that 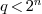 , hence fits in C.
, hence fits in C.
2.2.1.Modular product
Let  be an integer such that
be an integer such that 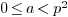 .
The remainder
.
The remainder 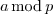 can be obtained as follows:
can be obtained as follows:
-
Decompose
 into
into 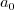 and
and
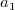 such that
such that 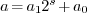 , with
, with 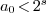 , and compute
, and compute 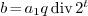 . From
. From 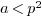 it follows that
it follows that 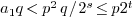 . So
. So 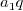 has size at most
has size at most  , and we
have
, and we
have 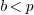 .
.
-
Compute
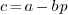 . From the definition of
. From the definition of 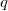 we have:
we have:
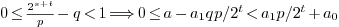 .
.
It follows that
 .
.
-
Let
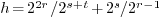 . From
. From 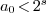 we deduce
that
we deduce
that 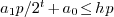 . It thus suffices to substract at most
. It thus suffices to substract at most
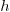 times
times 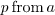 to obtain
to obtain 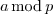 .
.
In general we can always take 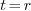 and
and 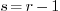 , so that
, so that 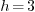 . For when
. For when 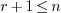 , it is better to take
, it is better to take 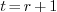 and
and 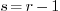 so that
so that  . Finally, for when
. Finally, for when
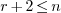 one can take
one can take 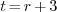 and
and 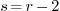 so that
so that 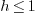 . These settings are
summarized in the following table:
. These settings are
summarized in the following table:
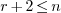 |
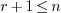 |
 |
|
 |
 |
 |
 |
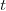 |
 |
 |
 |
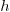 |
 |
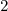 |
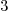 |
In these three cases remark that the integer 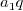 has size at most
has size at most 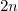 .
.
It is clear that the case 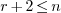 leads to the fastest
algorithm since step 3 reduces to one substraction/comparison that can
be implemented as min
leads to the fastest
algorithm since step 3 reduces to one substraction/comparison that can
be implemented as min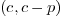 within type C
alone. A special attention must be drawn to when
within type C
alone. A special attention must be drawn to when 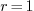 ,
that corresponds to
,
that corresponds to 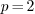 : we must suppose that
: we must suppose that 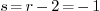 is indeed computed within an unsigned int type,
hence is sufficiently large to ensure
is indeed computed within an unsigned int type,
hence is sufficiently large to ensure 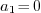 and
and  , hence the correctness of the algorithm.
, hence the correctness of the algorithm.
2.2.2.Numerical inverse
Let us now turn to the computation of the numerical inverse 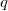 of
of 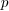 . The strategy presented here
consists in performing one long division in C followed
by one Newton iteration. Let
. The strategy presented here
consists in performing one long division in C followed
by one Newton iteration. Let 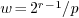 be the numerical
inverse of
be the numerical
inverse of 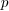 , normalized so that
, normalized so that 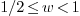 holds. Let
holds. Let 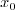 denote the initial
approximation, and
denote the initial
approximation, and 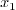 be its Newton iterate
be its Newton iterate 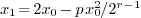 . If
. If 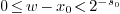 for some positive
integer
for some positive
integer 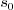 then it is classical that
then it is classical that 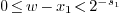 with
with 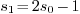 .
.
Under the assumption that 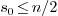 , we can compute a
suitable
, we can compute a
suitable 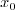 as the floor part of
as the floor part of 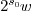 by the only use of operations within base type C. In
other words we calculate
by the only use of operations within base type C. In
other words we calculate 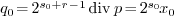 as follows:
as follows:
-
If
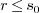 then
then 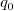 is obtained
by means of one division in C.
is obtained
by means of one division in C.
-
Otherwise
 . We decompose
. We decompose 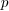 into
into 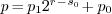 , with
, with  . Note
that
. Note
that 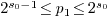 . Within C perform the
long division
. Within C perform the
long division 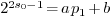 . By multiplying both side of
the latter equality by
. By multiplying both side of
the latter equality by 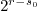 we obtain that
we obtain that 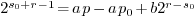 . From
. From  and
and 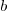 , we easily deduce
, we easily deduce 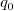 since
since 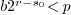 and
and 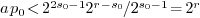 .
.
The computation of 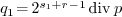 , that is the floor part of
, that is the floor part of
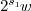 , then continues as follows:
, then continues as follows:
-
From the definition of
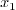 , one can write:
, one can write: 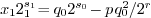 . We thus compute
. We thus compute 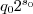 and the
ceil part of
and the
ceil part of 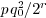 in order to deduce the floor
part
in order to deduce the floor
part  of
of 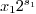 . Note that
. Note that
 fits C.
fits C.
-
From the above inequalities it follows that
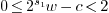 .
We thus obtain
.
We thus obtain 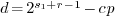 < 2p. If
< 2p. If 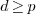 then return
then return 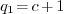 else return
else return 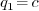 .
.
Finally, 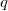 is deduced in this way:
is deduced in this way:
-
Set
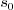 as (
as (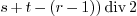 , and compute
, and compute
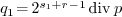 as just described.
as just described.
-
Note that
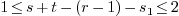 . If
. If 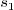 +1=
+1=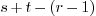 then
then 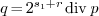 otherwise
otherwise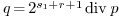 .
.
2.2.3.Modular product by a constant
Let 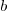 be a modulo
be a modulo 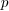 integer that is to be involved in several modular products. Then one
can compute
integer that is to be involved in several modular products. Then one
can compute 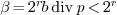 just once and obtain a speed-up
within the products by means of the follows algorithm:
just once and obtain a speed-up
within the products by means of the follows algorithm:
-
Compute
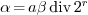 . It follows that
. It follows that 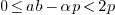 .
.
-
Compute
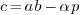 . If
. If 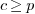 then
c=c+1. Return
then
c=c+1. Return  .
.
The computation of 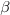 can be done as follows from
can be done as follows from
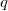 :
:
-
Compute
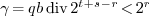 . Note that
. Note that 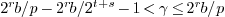 .
.
-
Since
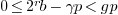 , with
, with 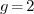 if
if 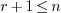 and
and 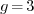 otherwise, deduce
otherwise, deduce
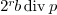 from
from 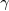 .
.
3.Further remarks
- On some processor architectures code to manipulate short int can be larger and slower than corresponding code which deals with int. This is particularly true on the Intel x86 processors executing 32 bit code. Every instruction which references a short int in such code is one byte larger and usually takes extra processor time to execute.
- Do not use char but signed char or unsigned char for the sake of portability.