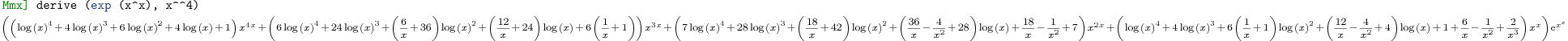The quest of modularity and efficiency
http://www.mathemagix.org/
|
|
|
Joris van der Hoeven &
Grégoire Lecerf & Bernard
Mourrain
|
|
|
|
Abstract. We describe the goals
and architecture of the software project Mathemagix,
the main list of packages it contains, the main characteristics of
its programming language and connections with existing front-end.
1.Context and objectives
Symbolic computation is usually associated with computer algebra systems
such as Maple or Mathematica.
These softwares are commercial products, with large communities of users
(several millions of users). They provide an interpreter of commands,
connected to a huge library of functionalities. Their development
started more than twenty years ago and evolved from academic projects
into large software companies. The connection with the academic domain
made it possible to integrate new algorithmic contributions from
researchers, whereas the software company effort concentrated on
graphical user interface developments. Concerning numerical computation,
Matlab is having a similar position, as a
commercial product with a large community of users, also integrating
academic contributions.
Though these softwares are equipped with high level programming
languages, their interpreters suffer from efficiency, especially when it
comes to dedicated and optimized computations. For this reason, several
special purpose C/C++ libraries have been developed, which have become
increasingly powerful for solving the tasks they were designed for
(Gmp, Mpfr, Pari,
Ntl, Macaulay, Singular,
Cocoa, Fgb,
etc.). In numerical computation, a similar evolution took
place, starting with the reference library Lapack.
Some of these systems are equipped with their own interpreter and a
corresponding programming language. Others are designed as libraries
which can be linked to high level applications.
Another approach to tackle the efficiency problem while implementing new
functionalities, adopted by Axiom (and Aldor) is to provide a compiler with the system, which
allows to produce more efficient code, that can be linked with the
interpreter or used independently.
In the recent years, we observed a new phenomena, with the appearance of
general purpose open source software such as Maxima,
Axiom, Octave, Scilab,
etc. Another new free software sage, based its
evolution on the capability to integrate different existing packages,
while providing an easy-to-use and homogeneous framework for command
evaluation and extension of the functionalities. For this purpose the
choice of Python as an extension language was
natural. The integration of external free packages was also observed in
commercial software such as Maple, which
incorporates for instance Gmp,
Mpfr or Lapack.
The main goals of the Mathemagix project are:
-
to provide a coherent framework for the development and publication of
efficient and stand-alone packages;
-
to provide packages, which implement in a very efficient way the basic
operations needed in algebraic and numeric computation;
-
to provide tools for the connection of these packages to other
interpreters, in particular to the Mathemagix
interpreter, or to other applications;
-
to provide a high-level programming language, adapted to mathematical
computation, an interpreter and a compiler;
-
to provide high level user interfaces, based on external tools such as
TeXmacs and Axel.
These goals are motivated by the will to develop implementations that
can be freely reused by the community, the need to build efficient
software based on stable and strong algorithmic foundations, the variety
of environments in which this implementation can be used, but also the
lack of sufficiently general compiled computer algebra languages and the
increasing request for using free computer algebra systems in our
scientific activities.
2.Platform architecture
To achieve modularity and scalability, Mathemagix
is organized as a collection of packages with dag-like dependencies.
Each of them provides a C++ interface for gluing
some of its functionalities to the Mathemagix
interpreter. It can also provide code written in the Mathemagix
language, or gluing code for the interaction with other applications
such as Axel.
A package is a library in the usual sense. It is devoted to a domain of
computation. To fit with the global architecture, its structure should
follow a certain template: The header files of a package (say pkg) are found in include/pkg; the source
files are found in src, the macros for the configuration
step are found in macros, the files for the connection
with the interpreter are in glue, the files for the
interpreter in mmx, the file used for the construction
steps are in build, and so on. The interpreter and
compiler of the language are provided by the packages mmxlight
and mathemagix, following this structure. They can be
built and used independently of most of the other packages.
To manage the collection of packages, we use a tool called automagix.
For each package, it can generate the list of headers files, or source
files needed to construct the different libraries and produce the
corresponding makefiles (build/Makefile.am). It can also
generate the configuration files (configure.ac) taking
into account the dependency with other packages following the Mathemagix structure or with external libraries. Its
behavior is specified by the file specif/pkg.amx. The
tool automagix also produces a global configuration and
makefile to configure and to build all the packages in an order
compatible with their dependencies. It also passes the different options
for the construction of the packages. This tool is written in the Mathemagix language, using its interpreter. It generates
tools which are compatible with the autotools suite, in
order to get portable and standalone configuration tools.
To generate automatically the glue for the interpreter, the tool autoglue (also written in the Mathemagix
language) can be used. It takes the Mathemagix
files (.mmx) of the directory glue and
produces the corresponding C++ files (.cpp)
for the glue. A Mathemagix glue file contains a
dictionary between the functions imported in the interpreter, described
by their signatures, and the corresponding C++
functions. Signatures with type parameters (templates in C++)
are allowed. The gluing C++ code of a function is
generated if all the types involved in its signature are specialized
(using the keyword specialize). The generated cpp
files can then be compiled and assembled in a dynamic library libmmxpkg.[so,dyl,...]
(automatically via automagix). All the functions
specialized in this glue library can then be used in the interpreter via
the command: use "pkg".
3.Packages
Most of the code of the packages is written in C++, the other part
behind mainly written in the Mathemagix language.
The current list of packages represents about 200,000 effective lines of
code. This list of packages is in constant evolution. We list here the
main ones:
-
basix
-
This package contains the basics, that is data structures for symbols,
lists, arrays, hash tables, etc. It also provides a system for generic
objects. Parsers and pretty printers, together with a system for
keeping track of locations in the source code and generating error
messages are also available there. Important operators for systematic
use throughout the project and the glue facility, both for
interpreters and functionality can also be found in this package.
-
numerix
-
It provides a C++ interface for extended arithmetic over integer,
rational numbers based Gmp and over floating
numbers based on Mpfr. Complexified version of
these types are also provided as well intervals and balls for
certified arithmetic. Modular numbers with preinverse computation, ...
are also provided in this package.
-
algebramix
-
This package aims to provide basic routines on univariate
polynomials, series and matrices with state-of-the-art asymptotic
time complexities.
| Mmx] |
bit_precision := 128; z: Series Floating == series (0,
1);
|
| Mmx] |
exp (exp z - 1) [25000]
compute 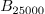 for for

|
-
multimix
-
This package is dedicated to transseries and optimize computation on
dense multivariate polynomials and series.

-
analyziz
-
This package contains tools for effective analytic computation,
including analytic continuation and manipulation of effective analytic
functions.
-
columbus
-
Visualization tool for analytic functions. Below, we have displayed
the solutions to two numerically unstable differential equations
(Chazy and Blasius). Each pixel in the image corresponds to a point
in the complex plane and the real and imaginary parts of the
function are indicated by intensities of two different colours. In
particular, the structure of the singularities of the function
becomes apparent.


-
linalg
-
This package provides basic linear algebra tools on dense matrices,
with approximate coefficients. An interface on Lapack
library is used for machine type coefficients.
-
multivariate
-
Different representations of multivariate polynomials are available in
this package. The sparse representation as an ordered sequence of
terms (or monomials) is parametrized by the monomial ordering. The
dense representations as tensor products either in the monomial or in
the Bernstein basis are also provided by this package.
-
realroot
-
Subdivision solvers for univariate polynomials using Bernstein or
Monomial basis representation. It includes a very efficient univariate
solver, which computes the continued fraction expansion of the real
roots of a polynomial. Subdivision solvers for multivariate
polynomials using Bernstein basis representation, sleeve approximation
and preconditioner are also available in this package.
-
polytopix
-
In this package, tools for the manipulation of polytopes are available
(representation by inequalities or by generators) and connection with
multivariate polynomial supports. The polytope manipulations are based
on the library Cdd. A plugin for Axel
is also available.
-
shape
-
This package provides data structures to manipulate algebraic curves
and surfaces which are given by equations or by a parametrization.
It also contains tools to compute, in a certified way, the topology
of these algebraic sets or to compute arrangements, (self-)
intersection curves of parametrized surfaces, singularities ... Here
is an example of a 3D curve obtained from the intersection of the
real part and imaginary part of associated with a planar curve in
the complex plane nearby a singular point.

-
symbolix
-
This package is for the manipulation of symbolic expressions. It
provides basic calculus: differentiation, substitution, ... on these
expressions.
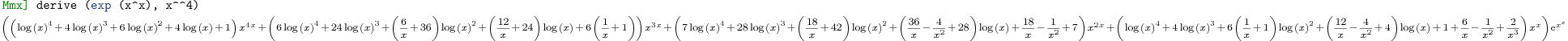
4.Towards a new high level language
The long term aim of the Mathemagix language is to
provide a new high level language, with the following characteristics:
-
Strong typedness
-
It is strongly typed, with support for overloading, implicit
conversions, generic objects, compile-time type checking and,
possibly, built-in support for expression types which interact with
the type system.
-
High level control structures
-
High level control structures, like coroutines, generators,
exceptions, continuations, etc.
-
Reusability of external libraries
-
Besides achieving runtime efficiency of Mathemagix
itself, we aim to achieve runtime efficiency through the extensive
reuse of existing dedicated libraries written in other languages.
Mathemagix therefore implements transparent
mechanisms for reusing external libraries and in particular C++
template libraries.
Currently, we provide a rather slow interpreter of only a part of the
full language (the mmxlight) package. A compiler
is under development (the mathemagix package).
5.Front-ends
-
A textual shell mode
-
Mathemagix provides the user with a usual ascii
shell mode and a convenient advanced programmer interface, based on a
dedicated emacs mode.
-
A graphical interface
-
It can be used within GNU TeXmacs as a primary graphical interface.
This offers a unified and user friendly framework for editing
structured documents with different types of content (text, graphics,
mathematics, etc.), including interactive content such as
Mathemagix sessions. The rendering engine uses
high-quality typesetting algorithms so as to produce professionally
looking documents, which can either be printed out or presented from a
laptop. It is also used to write and to generate the top-level
documentation of the packages in different format (html,
tex), in combination with Doxygen
for the C++ code documentation.
-
A geometric modeler
-
The program is connected to the algebraic-geometric modeler axel as a tool for visualisation and geometric
computation. Currently some packages of Mathemagix
are directly used to build the computational kernel of Axel
(multivariate, realroot, shape).
Other packages (eg. polytopix) are producing
independent plugins, which extend the interface and the
functionalities of the algebraic-geometric modeler. The connection
between the interpreter Mmx-light and Axel is under development, in order to get a
bidirectional interoperability of the two applications.
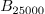 for
for