| The ultimate |
We plan to improve the current
- The declaration of a symbol is seen as a notification of the ability to carry out a certain task under certain circumstances. Several solutions may be specified for the same task under different circumstances (overloading and natural extensability).
-
Ambiguous expressions systematically carry types and
Mathemagix contains a general mechanism for computations with ambiguous types. - As a counterpart to the powerful constructs which are provided by the type system, the user has some responsability of using it in the appropriate way. When used inappropriately, some of the type checking algorithms may not terminate or abort prematurely.
- The type system should be as “independent” as possible from the rest of the language.
Concretely speaking,
- Atomic symbols
-
Examples:
 ,
,  , etc.
, etc.
- Type constructors
-
Example:
 , etc.. Type
constructors may also use instances, like in
, etc.. Type
constructors may also use instances, like in  .
.
- Logical constructors
-
Examples:
 (overloaded
(overloaded  and
and  ),
), 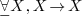 (template
type).
(template
type).
Let us explain these ideas in a bit more detail.
Logical supertypes
In classical type systems, each variable  has a
type
has a
type 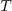 (written
(written 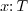 ). In
). In
 of type
of type
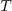 ” (written
” (written 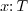 ) as a
statement. Such statements may be combined in the language of
first order logic. Now logical supertypes are new types which
correspond to such combinations. For instance, the type
) as a
statement. Such statements may be combined in the language of
first order logic. Now logical supertypes are new types which
correspond to such combinations. For instance, the type  is the type such that for all symbols
is the type such that for all symbols  ,
we have
,
we have

In other words, if 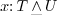 in a given context, then
in a given context, then
 may both be used as an object of type
may both be used as an object of type 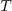 or as an object of type
or as an object of type 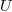 ,
i.e.
,
i.e.  has been overloaded, or the
result of an ambiguous expression. The following logical type
constructors are currently implemented in the type system (although
only
has been overloaded, or the
result of an ambiguous expression. The following logical type
constructors are currently implemented in the type system (although
only 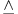 and
and  are currently
available in the interpreter):
are currently
available in the interpreter):
-
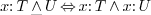 for overloading.
for overloading.
-
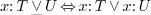 for union-like types.
for union-like types.
-
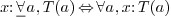 for template types. For instance, if
for template types. For instance, if  , then for any type
, then for any type 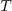 , we
may use
, we
may use  as a function from
as a function from 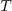 to
to 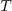 .
.
-
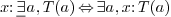 for generic types. For instance, a routine
to find the roots of a polynomial might have the type
for generic types. For instance, a routine
to find the roots of a polynomial might have the type  .
.
In the future, we also plan to add conditional types 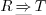 ,
with
,
with 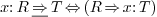 . The relations
. The relations 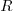 should be defined using first order logic axioms (and possibly refer
to predicate routines). For instance, this would permit to use types
like
should be defined using first order logic axioms (and possibly refer
to predicate routines). For instance, this would permit to use types
like 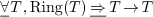 .
.
Extensibility and exceptions
The advantage of logical supertypes is that it is possible to define functions which are only valid under very precise circumstances, which are modelized using first order logic. This makes the system very extensible and customizable.
Indeed, assume for instance that you have functions  and
and 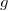 , where
, where 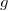 depends on
depends on
 and where
and where  is valid
under certain circumstances. Then it may be that someone makes a new
implementation of
is valid
under certain circumstances. Then it may be that someone makes a new
implementation of  under another circumstance.
Then it becomes automatically possible to apply
under another circumstance.
Then it becomes automatically possible to apply 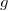 in this new circumstance.
in this new circumstance.
It may also be that the original implementation of  is valid under very broad hypothesis, but also very unefficient. Then
a new user may reimplement
is valid under very broad hypothesis, but also very unefficient. Then
a new user may reimplement  under more
particular hypothesis later. Here
under more
particular hypothesis later. Here 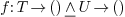 is applied to
is applied to 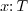 ,
and the typechecker can prove
,
and the typechecker can prove 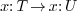 , but not
, but not  , then
, then 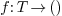 is applied. It should
be noticed that this principle makes it unnecessary to introduce
negation in the logical type system. In fact, negation would be
harmful, because it breaks the extensibility.
is applied. It should
be noticed that this principle makes it unnecessary to introduce
negation in the logical type system. In fact, negation would be
harmful, because it breaks the extensibility.
Another major advantange of the logical supertype approach is that it
allows for less hierarchic design of big projects. For example,
consider the problem where you have trees with 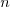 types of possible nodes and that you need to define
types of possible nodes and that you need to define 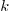 types of actions on trees which depend on the nodes, but where many
implementations can be grouped on either node type or action type. In
types of actions on trees which depend on the nodes, but where many
implementations can be grouped on either node type or action type. In
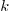 virtual functions, which makes it possible to regroup the
implementations by node types, or you declare a simple tree class with
enumeration nodes, and you regroup the implementations by their action
type. In either case, one design style is priviledged: dispatching on
node type or dispatching on action type. In
virtual functions, which makes it possible to regroup the
implementations by node types, or you declare a simple tree class with
enumeration nodes, and you regroup the implementations by their action
type. In either case, one design style is priviledged: dispatching on
node type or dispatching on action type. In
Feasability
Of course, it is nice to design a very powerful type system, but it is also nice if one can implement it. In the most general setting of first order logic, this is quite hopeless. Nevertheless, only a tiny part of the first order logic is used in practice, even though it may be hard to indentify this part. Our approach is to progressively extend the strength of the implementation of the type system and accept the fact that it will not do everything. This should make certain types of uses perfectly reliable, but it will remain up to the user not to abuse the type system.
In order to make this philosophy fully functional, it is nice to make
the type system as independent as possible from the rest of the
language, so that it might actually be carried out by a dedicated
systeem, like a theorem proving system. In
At the moment, the type system is able to handle pure predicate logic
(restricted to 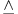 and
and  )
well. It can also deal with types of the form
)
well. It can also deal with types of the form
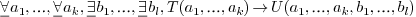
in a systematic way, and conjunctions of such types. Many easy other types can also be dealt with, though not systematically. A current limitation is that when you have a method
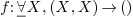
and an implicit converter 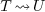 , then
, then  can not yet be applied to
can not yet be applied to 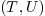 .
.
Semantics
The precise semantics of logical supertypes is still under
development. One has to decide in particular if one wants to restrict
the application of quantifiers to atomic supertypes (i.e.  ,
,  or
or  are
OK, but not
are
OK, but not  ). Indeed, consider the function
). Indeed, consider the function
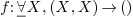
If one may take 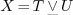 , then, using the convertions
, then, using the convertions
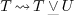 and
and 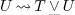 , it becomes
possible to applie
, it becomes
possible to applie  to
to 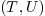 since this is the case for all
since this is the case for all 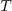 and
and 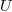 , we obtain an implicit converter
, we obtain an implicit converter
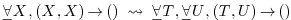 |
(1) |
Here one hits the limitations of the approach of not requiring any
additional information on types, like a category in
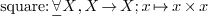
then it is not really necessary to know the type of 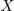 ,
since it is very likely that the user will only apply it in the case
when there is a multiplication defined on
,
since it is very likely that the user will only apply it in the case
when there is a multiplication defined on 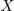 .
However, if one has multiplications on
.
However, if one has multiplications on 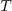 and
and
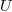 , then it is highly unlikely to have a
multiplication on
, then it is highly unlikely to have a
multiplication on  , so the implicit conversion
(?) is generally abusive.
, so the implicit conversion
(?) is generally abusive.