SYNAPS (SYmbolic Numeric ApplicationS) » Tutorial

Geometric computation

The aim of this section is to build functions, which given two rational surfaces on a bounded domain, allow us to compute their intersection and visualise the result. Fur this purpose, we will use the visualisation tool axel.

Rational surfaces

A rational surface is defined by a map

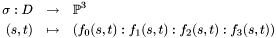
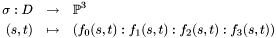
$\begin{eqnarray*} \sigma : D & \rightarrow & \mathbbm{P}^3\\ (s, t) & \mapsto & (f_0 (s, t) : f_1 (s, t) : f_2 (s, t) : f_3 (s, t)) \end{eqnarray*}$

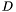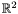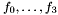where $D$ is a domain of $\mathbbm{R}^2$ (in geometric modeling applications, usually $[0, 1]^2$ ) and $f_0, \ldots, f_3$ are polynomials. The data structures for these rational maps is defined in

#include <synaps/shape/surface/MPDrationalSurface.h>

It can be defined easily from strings, as illustrated below:

# include <synaps/shape/interfaces/IRationalSurface.h>
# include <synaps/shape/surfaces/MPDRationalSurface.h>


int main(int argc, char** argv) 
{
  using std::cout;
  using std::endl;
  MPolDseRationalSurface<double> s1, s2;

  s1.setEquations("s^2+t^2+1", "s-1+t^2", "s^2", "t^2", "s t");
  s1.setRange(-1, 1, -1, 1);

  s2.setEquations("s^2+t^2+1", "s*t-1", "t^2", "1-s^2", "s t");
  s2.setRange(-1, 1, -1, 1);

  cout<<s1<<endl;
  cout<<s2<<endl;

}

Visualisation

In order to visualised these objects, one can use the connection files for axel:

#include <synaps/base/io/axel.h>

This defines a axel ostream, which can be used as follows:

 axel::ostream vw("tmp.axl");
 vw<< s1;
 vw<<Color(25,25,225);
 vw<<s2;
 vw.view();

In the construction of the viewer vw, tmp.axl is the name of the file where the data are stored. Then we send s1 to this view and visualise. We modify the color used to print the objects by using os<<Color(25,25,225); The color is describe in (red,green,blue) format with a integer number between 0 and 255. The surface s2 is printed, with this color. The view is displayed by the command vw.view(). It yields

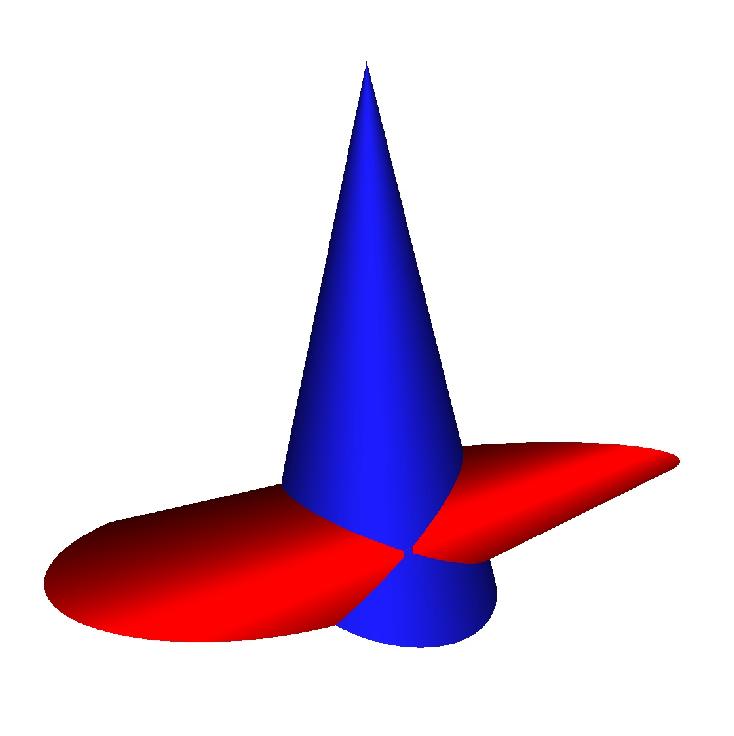
# include <synaps/shape/interfaces/IRationalSurface.h>
# include <synaps/shape/surfaces/MPDRationalSurface.h>
# include <synaps/shape/surfaces/axel.h>


int main(int argc, char** argv) 
{
  using std::cout;
  using std::endl;
  MPolDseRationalSurface<double> s1, s2;

  s1.setEquations("s^2+t^2+1", "s-1+t^2", "s^2", "t^2", "s t");
  s1.setRange(-1, 1, -1, 1);

  s2.setEquations("s^2+t^2+1", "s*t-1", "t^2", "1-s^2", "s t");
  s2.setRange(-1, 1, -1, 1);

  axel::ostream vw("tmp.axl");
  vw<<s1;
  vw<<Color(25,25,225);
  vw<<s2;
  vw.view();
}

Intersection

Given two such surfaces $s_1$

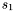and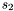

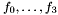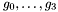, given by the polynomials $f_0, \ldots, f_3$ and $g_0, \ldots, g_3$ , we want to compute their intersection points defined by the system:

$(1) \left\{ \begin{array}{l} g_1 (u, v) f_0 (s, t) - f_1 (s, t) g_0 (u, v) = 0\\ g_2 (u, v) f_0 (s, t) - f_2 (s, t) g_0 (u, v) = 0\\ g_3 (u, v) f_0 (s, t) - f_3 (s, t) g_0 (u, v) = 0 \end{array} \right.$

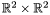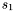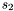This defines a curve in $\mathbbm{R}^2 \times \mathbbm{R}^2$ which image by $s_1$ or $s_2$ in the intersection of the surfaces.

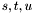In order to visualise this intersection curve, we are going to fixe the values of $v \in [0, 1]$ and to solve the corresponding system in $s, t, u$ and then compute the image of these points by $s_1$ .

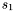We are going to use the function intersect, which applies for anay paramteric surface. Its arguments are converted to pointers to IParametricSurface type. The result is of type IGLGood. It corresponds to a piecewise linear approximation of the result.

# include <synaps/shape/surfaces/MPDRationalSurface.h>
# include <synaps/shape/interfaces/IGLGood.h>
# include <synaps/shape/surfaces/axel.h>

int main(int argc, char** argv) 
{
  using std::cout;
  using std::endl;
  MPolDseRationalSurface<double> s1, s2;

  s1.setEquations("s^2+t^2+1", "s-1+t^2", "s^2", "t^2", "s t");
  s1.setRange( -1, 1, -1, 1);

  s2.setEquations("s^2+t^2+1", "s*t-1", "t^2", "1-s^2", "s t");
  s2.setRange(  -1., 1., -1., 0.5);
  
  axel::ostream vw("tmp.axl");
  vw<<s1;
  vw<<Color(25,25,225);
  vw<<s2;
  IShape * r=intersect(&s1,&s2);
  IGLGood* g= r->mesh();
  vw << *g;
  vw.view();

}

Here is what we otain for the previous surfaces s1, s2:

SYNAPS DOCUMENTATION