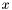 in
in 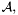
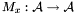 defined by
defined by 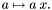 It is straightforward to check that the matrix of
It is straightforward to check that the matrix of 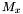 in the basis
in the basis 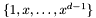 is given by
is given by  be any field and suppose given a polynomial
be any field and suppose given a polynomial 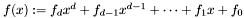 in
in ![$\mathbbm{K}[x]$](form_115.png) . Using the standard Euclidean polynomial division it is easy to see that the quotient algebra
. Using the standard Euclidean polynomial division it is easy to see that the quotient algebra ![$\mathcal{A} = \mathbb{K} [x] / I$](form_116.png) , where
, where 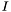 denotes the principal ideal of
denotes the principal ideal of ![$\mathbbm{K}[x]$](form_115.png) generated by the polynomial
generated by the polynomial 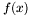 , is a vector space over
, is a vector space over 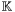 of dimension
of dimension 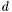 with canonical basis
with canonical basis 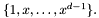
Consider the multiplication by 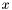 in
in 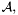
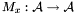 defined by
defined by 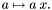 It is straightforward to check that the matrix of
It is straightforward to check that the matrix of 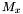 in the basis
in the basis 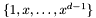 is given by
is given by
![\[ M_x = \left[ \begin{array}{cccc} 0 & \cdots & 0 & - f_0 / f_d\\ 1 & \ddots & & \vdots\\ \vdots & & 0 & \vdots\\ 0 & & 1 & - f_{d - 1} / f_d \end{array} \right] \]](form_125.png)
(the column on the far right corresponds to the Euclidean division of 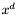 by
by 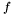 ). Therefore the characteristic polynomial of
). Therefore the characteristic polynomial of 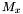 equals
equals 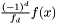 and the roots, with their corresponding multiplicities, of the polynomial
and the roots, with their corresponding multiplicities, of the polynomial 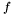 can be recovered by computing the eigenvalues of the multiplication map
can be recovered by computing the eigenvalues of the multiplication map 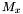 . See e.g. [Lang02].
. See e.g. [Lang02].
synaps/upol/resultant.h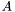 be a commutative ring, which is assumed to be a domain, and suppose given two polynomials in
be a commutative ring, which is assumed to be a domain, and suppose given two polynomials in ![$A [x]$](form_129.png) of respective degree
of respective degree 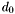 and
and 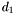
![\[ \begin{array}{l} f_0 (x) : = c_{0, 0} + c_{0, 1} x + \cdots + c_{0, d_0} x^{d_0},\\ f_1 (x) : = c_{1, 0} + c_{1, 1} x + \cdots + c_{1, d_1} x^{d_1} . \end{array} \]](form_132.png)
The Sylvester matrix of 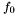 and
and 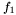 (in degree
(in degree 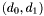 ) is the matrix whose columns contain respectively the coefficients of the polynomials
) is the matrix whose columns contain respectively the coefficients of the polynomials 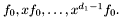
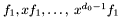 expanded in the monomial basis
expanded in the monomial basis 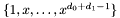 . It is a square matrix of size
. It is a square matrix of size 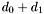 which has the following form:
which has the following form:
![\[ S = \begin{array}{ll} \left( \begin{array}{ccc|ccc} c_{0, 0} & & 0 & c_{1, 0} & & 0\\ \vdots & \ddots & & \vdots & \ddots & \\ & & c_{0, 0} & & & c_{1, 0}\\ c_{0, d_0} & & \vdots & c_{1, d_1} & & \vdots\\ & \ddots & \vdots & & \ddots & \vdots\\ 0 & & c_{0, d_0} & 0 & & c_{1, d_1} \end{array} \right) & \begin{array}{l} 1\\ x\\ \vdots\\ \vdots\\ \vdots\\ x^{d_0 + d_1 - 1} \end{array} \end{array} \]](form_140.png)
More precisely, it is the matrix of the 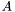 -linear map
-linear map
![\begin{equation} \anchor UResultantphi \begin{array}{rrl} \sigma : A [x]_{< d_1} \oplus A [x]_{< d_0} & \rightarrow & A [x]_{< d_0 + d_1}\\ (q_0, q_1) & \mapsto & f_0 q_0 + f_1 q_1 \end{array} \end{equation}](form_141.png)
in the monomial bases 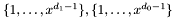 and
and 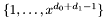 , where
, where ![$A [x]_{< k}$](form_144.png) denotes the set of polynomials in
denotes the set of polynomials in ![$A [x]$](form_129.png) of degree lower or equal to
of degree lower or equal to 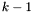 .
.
Proposition: If 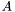 is a field, then we have the equality is a field, then we have the equality 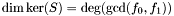 . . |
Definition: The resultant of the polynomials 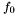 and and 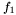 , denoted , denoted 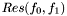 , is the determinant of the Sylvester matrix of , is the determinant of the Sylvester matrix of 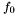 and and 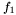 |
The resultant 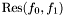 is thus an element in
is thus an element in 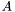 . It has been widely studied in the literature, since it provides a way to eliminate the variable
. It has been widely studied in the literature, since it provides a way to eliminate the variable 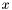 from the polynomial system
from the polynomial system 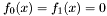 . Indeed, we have
. Indeed, we have
Proposition: 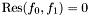 if and only if either if and only if either 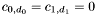 , or either , or either 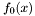 and and 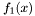 have a common root in the algebraic closure of the fraction field have a common root in the algebraic closure of the fraction field 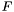 of of 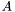 (or equivalently (or equivalently 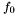 and and 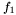 are not coprime in are not coprime in ![$F [x]$](form_155.png) ). ). |
synaps/upol/resultant.h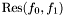 . We now suppose w.l.o.g. that
. We now suppose w.l.o.g. that 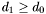 .
.
Definition: The Bezoutian of the polynomials 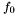 and and 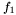 is the element in is the element in ![$A [x, y]$](form_157.png) defined by defined by
and the Bezout matrix is |
The matrix 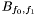 is a
is a 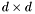 -matrix which is symmetric:
-matrix which is symmetric:
![\[ B_{f_0, f_1} = \left[ \begin{array}{ccc} \theta^{f_0, f_1}_{0, 0} & \cdots & \theta^{f_0, f_1}_{0, d - 1}\\ \vdots & & \vdots\\ \theta^{f_0, f_1}_{d_{} - 1, 0} & \cdots & \theta^{f_0, f_1}_{d - 1, d - 1} \end{array} \right] \]](form_162.png)
where 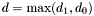 (
(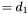 here).
here).
It is thus a smaller matrix than the Sylvester matrix, but has more complicated entries, and its determinant still equals the resultant of 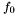 and
and 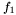 (up to a power of
(up to a power of 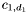 ):
):
|
Proposition: [Kra95] We have:
Moreover, if |
synaps/upol/resultant.h#include <synaps/upol.h> #include <synaps/linalg/MatrDse.h> #include <synaps/upol/resultant.h> typedef UPolDse<double> upol_t typedef MatrDse<double> matr_t; using std::cout; using std::endl; int main (int argc, char **argv) { using std::cout; using std::endl; upol_t p0("3*x0+3;"); double u1[]={2,0,-1,1};upol_t p1(u1,u1+4); cout <<"p0 ="<<p0<<endl<<"p1 ="<<p1<<endl;
![\[ p 0 = 3 x + 3, p 1 = x^3 - x^2 + 2 \]](form_168.png)
matrix_t S = sylvester<matr_t>(p0,p1); cout <<S<<endl;
![\[ \left[ \begin{array}{cccc} 3 & 0 & 0 & 2\\ 3 & 3 & 0 & 0\\ 0 & 3 & 3 & - 1\\ 0 & 0 & 3 & 1 \end{array} \right] \]](form_169.png)
matrix_t B = bezout<matr_t>(p0,p1); cout <<B<<endl;
![\[ \left[ \begin{array}{ccc} - 6 & - 3 & 3\\ - 3 & 0 & 3\\ 3 & 3 & 0 \end{array} \right] \]](form_170.png)
B = companion<matr_t>(p1); cout <<B<<endl;
![\[ \left[ \begin{array}{ccc} 0 & 0 & - 2\\ 1 & 0 & 0\\ 0 & 1 & 1 \end{array} \right] \]](form_171.png)
}
 |