![$f \in \mathbbm{R}[x]$](form_193.png) and
and ![$S (x) = [f (x), f' (x), S_2 (x), \ldots, S_N (x)]$](form_194.png) be the Sturm sequence of
be the Sturm sequence of 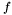 and
and 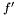 (x). Let
(x). Let 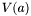 be the number of sign variation of
be the number of sign variation of 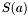 for
for 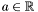 . Then, for any
. Then, for any 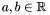 ,
, 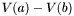 is the number of roots in ]a,b[.
is the number of roots in ]a,b[.
Theorem: Let ![$f \in \mathbbm{R}[x]$](form_193.png) and and ![$S (x) = [f (x), f' (x), S_2 (x), \ldots, S_N (x)]$](form_194.png) be the Sturm sequence of be the Sturm sequence of 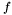 and and 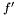 (x). Let (x). Let 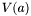 be the number of sign variation of be the number of sign variation of 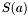 for for 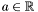 . Then, for any . Then, for any 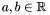 , , 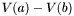 is the number of roots in ]a,b[. is the number of roots in ]a,b[. |
This leads to the following schema of algorithms, (which applies event to polynomials with multiple roots):
Algorithm: Isolation of the roots of 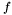 on the interval on the interval ![$[a, b]$](form_183.png) . .
INPUT: A polynomial
![$[a, b]$](form_183.png) containing exactly one real root of containing exactly one real root of 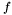 . . |
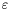 specified by the solver
specified by the solver SlvSturm. The default value is 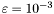 . If we want a specific precision
. If we want a specific precision 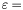
eps, we can use the following construction: solve(p, SlvSturm<O,C>(eps)).O, corresponding to the first parameter O of this class.C is the type of coefficients used during the computation. The default type is the type QQ of rational numbers. \p of type UPOL, is supposed to be given with exact coefficients. It is converted to a polynomial of type UPolDse<C>, if needed.synaps/usolve/sturm/SlvSturm.h.Seq< Interval<O> > solve(const UPOL& p, IslSturm<O,C> mth);
O, containing one and only one root of p.C is the type of coefficients used during the computation. The default type is the type QQ of rational numbers. \p of type UPOL, is supposed to be given with exact coefficients. It is converted to a polynomial of type UPolDse<C>, if needed.synaps/usolve/sturm/IslSturm.h.![]()
![]()
#include <synaps/upol.h> #include <synaps/arithm/QQ.h> #include <synaps/usolve/sturm/IslSturm.h> int main() { using std::cout; using std::endl; UPolDse<QQ> P("2*x^7+3*x^6+2*x^5+x^4-x^3-2*x^2-3*x+1"); cout <<"Testing: "<<P<<endl; //| Testing: 2*x^7+3*x^6+2*x^5+1*x^4-1*x^3-2*x^2-3*x+1 cout <<solve(P,IslSturm<QQ>())<<endl; //| [ -5/2,0 ], [ 0,5/8 ], [ 5/8,5/4 ] cout <<solve(P,IslSturm<QQ>(),0,1)<<endl; //| [ 0,1/2 ], [ 1/2,1 ] }
 |