![\[ \left\{ \begin{array}{l} f_1 (x_1, \ldots, x_n) = 0\\ \vdots\\ f_s (x_1, \ldots, x_n) = 0 \end{array} \right. \]](form_367.png)
We consider here the problem of computing the solutions of a system
![\[ \left\{ \begin{array}{l} f_1 (x_1, \ldots, x_n) = 0\\ \vdots\\ f_s (x_1, \ldots, x_n) = 0 \end{array} \right. \]](form_367.png)
in the case where such a system has a finite number of solutions in 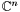 . The method developped in [PhT02] is implemented here. It proceeds in two steps
. The method developped in [PhT02] is implemented here. It proceeds in two steps
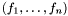 .
. is the following:
is the following:
From this normal form 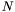 , we deduce the roots of the system as follows. We use the properties of the operators of multiplication by elements of
, we deduce the roots of the system as follows. We use the properties of the operators of multiplication by elements of 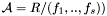 . For any
. For any 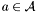 , we define
, we define
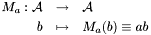
We also consider its transpose operator
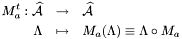
The matrix of 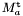 in the dual basis of a basis
in the dual basis of a basis 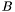 of
of 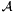 is the transpose of the matrix of
is the transpose of the matrix of 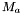 in
in 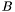 .
.
Our approach to solve polynomial systems is based on the following fundamental theorem:
Theorem: [AuSt88] [BMr98]Assume that 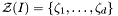 . We have . We have
|
Since 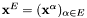 is a basis of
is a basis of 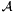 , the coordinates of
, the coordinates of 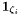 in the dual basis of
in the dual basis of 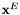 are
are 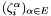 . Thus if
. Thus if 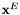 contains
contains 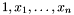 (which is often the case), we deduce the following algorithm:
(which is often the case), we deduce the following algorithm:
simple roots)}
Let 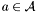 such that
such that 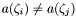 if
if 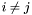 (which is generically the case) and
(which is generically the case) and 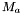 be the multiplication matrix by
be the multiplication matrix by 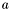 in the basis
in the basis 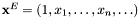 of
of 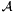 .
.
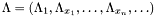 of
of 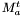 .
.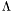 with
with 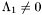 , compute and return the point
, compute and return the point 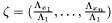 .
.template<class C> Seq<VectDse<std::complex<double> > > solve(L,Newmac<C>);
C is the type of coefficient in which we want to compute the normal form,synaps/msolve/Newmac.h.![]()
![]()
#include <synaps/arithm/gmp.h> #include <synaps/mpol.h> #include <synaps/base/Seq.h> #include <synaps/msolve/Newmac.h> typedef MPol<RR> mpol_t; int main (int argc, char **argv) { using namespace std; mpol_t p("x0^2*x1-x0*x1-1"), q("x0^2-x1^3-1"); std::list<mpol_t> I; I.push_back(p); I.push_back(q); cout << solve(I, Newmac<RR>())<<endl; //| [ (0.421134,0.779225) (-1.15111,0.166259) ] //| [ (0.421134,-0.779225) (-1.15111,-0.166259) ] //| [ (1.24525,-0.588209) (-0.0526987,1.13817) ] //| [ (-0.424222,0.478962) (0.405487,0.957865) ] //| [ (1.24525,0.588209) (-0.0526987,-1.13817) ] //| [ (-0.424222,-0.478962) (0.405487,-0.957865) ] //| [ (1.5648,3.86247e-19) (1.13148,8.13152e-19) ] //| [ (-1.04912,-1.30962e-18) (0.465166,-1.41031e-19) ] // The result is a sequence of vectors with coefficients of type // complex<double>. The columns correspond to the coordinates // of the roots (here x0, x1). The rows correspond to the roots // of the system (here 8 roots, with 2 which are real). }
 |