The multivariate polynomials
template<class C,
class O=Dlex,
class R=std::list<Monom<C,dynamicexp<'x'> > > >
struct MPol<C,O,R>;
are parameterised by
- the type of coefficients
C,
- the order used on the monomials
O. The default is the degree lexicographic ordering Dlex,
- the internal representation of the polynomials
R. The default is the list of monomials, with exponents of type dynamicexp<'x'>.
The containers R for this class could be list, vector, ... or any container with the member function insert.


#include <synaps/mpol.h>
typedef MPol<double> mpol_t;
typedef mpol_t::monom_t mon_t;
int main (int argc, char **argv)
{
using namespace std;
mpol_t p0("x1+x2+1"), p1("x2+x1^2+1");
cout<<p0<<", "<<p1<<endl;
mpol_t p2(p0+p1); cout<<p2<<endl;p2+=p1-p0; cout<<p2<<endl;
p2+=p1-p0; cout<<p2<<endl;
p2 =p0-p1; cout<<p2<<endl;
p2=p0 -p1*mon_t(2); cout<<p2<<endl;
}
x0, x1, x2, ... But one can use specific variable environments, in order to precise which variables we want to consider. The class Variables which implements such dictionnary between the internal variables xi and the one we want, can be used either when constructing a polynomial or when printing it. For instance, defines a dictionnary V where the variable u is x0, v is x1 so that the polynomial p which is constructed from the string "u\^{ </tt>2+..."} is in fact: The name of the variables can be recovered from their indices {V[0], V[1]}. If new variable names are used when constructing a polynomial, they are added to the dictionnary V, in the order they are parsed: Now V[2] is w, and V[3] the variable t. Notice, that here if we use an index 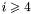 , we get for
, we get for V[i], the variable xi. In order to print the polynomial, with the appropriate variable names, instead of the operator <<, one can use the following functions: \ In this example, it yields: 

#include <synaps/mpol.h>
typedef MPol<double> mpol_t;
int main(int argc, char** argv)
{
Variables V("u v");
mpol_t p("u^2+v*u-v+2*u-1",V);
std::cout << p<< std::endl;
std::cout<<V[0]<<std::endl;
std::cout<<V[1]<<std::endl;
MPol<double> q("u^3-w+t", V);
std::cout<<V[2]<<std::endl;
std::cout<<V[3]<<std::endl;
std::cout<<V[4]<<std::endl;
Variables W("a b c d");
print(std::cout,p,W)<<std::endl;
print(std::cout,p)<<std::endl;
}
Different ordering on monomials are available:
Lex which corresponds to the lexicographic ordering, with 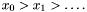
DegLex which corresponds to the degree and lexicographic ordering.
They provide the operator(m1,m2) and less(m1,m2) which compare two monomials m1, m2, using the functions m[i] and m.size().
![]()
![]()
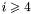 , we get for
, we get for