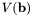 of
of ![$\mathbf{b}= [b_i]_{i = 0, \ldots, d}$](form_176.png) bounds the number of real roots of f on
bounds the number of real roots of f on ![$[0, 1]$](form_180.png) and is equal to it modulo 2.
and is equal to it modulo 2.
- If
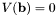 , the number of real root on [0, 1] is 0
, the number of real root on [0, 1] is 0
- If
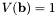 , the number of real root on [0, 1] is 1.
, the number of real root on [0, 1] is 1.
 in the Bernstein basis:
in the Bernstein basis: 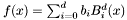 , where
, where 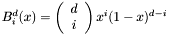 .The coefficients
.The coefficients ![$\mathbf{b}= [b_i]_{i = 0, \ldots, d}$](form_176.png) in this basis are called the control coefficients. We denote by
in this basis are called the control coefficients. We denote by  the number of sign variation of sequence
the number of sign variation of sequence  , not taking into account the
, not taking into account the 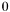 of this sequence. Descartes' rule applies on this representation as follows:
of this sequence. Descartes' rule applies on this representation as follows:
Proposition: The number of sign changes 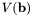 of of ![$\mathbf{b}= [b_i]_{i = 0, \ldots, d}$](form_176.png) bounds the number of real roots of f on bounds the number of real roots of f on ![$[0, 1]$](form_180.png) and is equal to it modulo 2. and is equal to it modulo 2.
|
We also use de Casteljau subdivision algorithm to subdivide the representation. This yields the following algorithm:
Algorithm: Isolation of the roots of 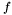 on the interval on the interval ![$[a, b]$](form_183.png) . .
INPUT: A representation
![$[a, b]$](form_183.png) containing exactly one real root of containing exactly one real root of 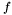 or intervals of size or intervals of size 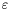 containing a containing a 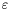 -multiple root. -multiple root. |
Several implementations, based on this scheme are available. The methods which compute the roots, within a given precision are named Slv..., those which isolate the roots are named Isl.... We describe now the solvers of these families available in the library.
O precises the type of the solutions, and C is the number type used to perform this computation. It is not necessarly the type of the coefficients of p, but it should be a field type. The default value of C is double so that it can be used as SlvBzStd<O>().SlvBzStd<O,C>(1e-10). The default type for this precision 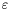 is
is double and the default value is 1e-6. If one want to use another type of precision (say X), one can use instead SlvBzStd<O,C,X>(xeps);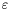 specificied by the class
specificied by the class SlvBzStd<O,C> and output in the result the middle of the interval. The subintervals which are removed have no sign variation. The \ intervals which are kept may have a sign variation bigger that 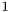 . The sequence
. The sequence s contains the approximated roots in increasing order.[a,b] (where a and b are of type O): \ solve(p,SlvBzStd<O,C>(),a,b);C=double for instance, or with exact arithmetic (eg. rational numbers C=QQ) to get certified approximation.synaps/usolve/bezier/SlvBzStd.hSeq<Interval<O> > solve(const UPOL& p, IslBzStd<O,C> mth);
p, that is, it computes a sequence of intervals containg a unique root, or an interval of size 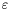 , where
, where 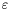 is the precision defined in in the class
is the precision defined in in the class IslBzStd<O,C>, if p has mutiple roots or a cluster of roots. This precision 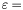
eps is specified by IslBzStd<O,C>(eps).O. The type C is the number type used during the computation. It is not necessarly the type of the coefficients of p, but it should be a field type. The default value of C is double so that it can be used as IslBzStd<O>().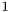 . If there is a multiple or a cluster of roots, the recursion will be continue until the size of the subinterval is smaller that the precision
. If there is a multiple or a cluster of roots, the recursion will be continue until the size of the subinterval is smaller that the precision 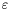 specificied by the class
specificied by the class IslBzStd<O,C>. The subintervals which are removed have no sign variation. The intervals kept, which are os size 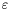 may have a sign variation bigger that
may have a sign variation bigger that 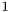 . The sequence
. The sequence s contains the subintervals sorted in increasing order. These intervals may share some ending points.[a,b] (where a and b are of type O): \ solve(p,IslBzStd<O,C>(),a,b);synaps/usolve/bezier/IslBzStd.h
SlvBzStd, except that the internal coeffcient type used to perform the subdivision is the integer type ZZ. The de Casteljau algorithm is adapted so that the representation of the internal polynomial remains with integer coefficients.O is the output type of the solutions; the precision 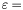
eps can be specified by SlvBzInteger<O>(eps).[a,b] (where a and b are of type O): solve(p,SlvBzInteger<O>(),a,b);synaps/usolve/bezier/IslBzInteger.h
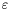 . The parameter
. The parameter O specifies the output type, for the approximate solutions.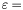
eps of the approximation can be given as an argument of the constructor: SlvBzBdg<O>(eps). The default type for this precision 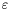 is
is double and the default value is 1e-6.double. The subdivision is performed, exploiting the coefficient sign variations on this upper and lower enveloppes of the input polynomial. If these polynomial enveloppes do not allow us to approximate the roots within the precision 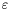 , we obtain a suspect subinterval (of size bigger than
, we obtain a suspect subinterval (of size bigger than 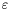 ) on which the solver
) on which the solver SlvBzInteger is applied.synaps/usolve/bezier/SlvBzBdg.hO solve(const UPOL& p, SlvRkw<O,C> mth);
p, using Rockwood's method. The internal type used during the computation is C, which default value is double.
eps of the approximation is an argument of the constructor: SlvRkw<O,C>(eps). The default type for this precision 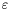 is
is double and the default value is 1e-6.synaps/usolve/bezier/SlvRkw.h![]()
![]()
#include <synaps/upol.h> #include <synaps/arithm/QQ.h> #include <synaps/usolve/bezier/SlvBzStd.h> #include <synaps/usolve/bezier/IslBzStd.h> #include <synaps/usolve/bezier/SlvRkw.h> int main() { using std::cout; using std::endl; UPolDse<ZZ> P("2*x0^7+3*x0^6+2*x0^5+1*x0^4-1*x0^3-2*x0^2-3*x0+1"); cout <<"Testing: "<<P<<endl; //| Testing: 2*x^7+3*x^6+2*x^5+1*x^4-1*x^3-2*x^2-3*x+1 cout <<solve(P,SlvBzStd<double,double>(1e-6))<<endl; //| -1.35142, 0.278212, 0.880286 cout <<solve(P,IslBzStd<double,double>(1e-6))<<endl; //| [ -1.35143,-1.35142 ], [ 0.278212,0.278213 ], //| [ 0.880286,0.880287 ] cout << solve(P,SlvRkw<double>(1e-6)) <<endl; //| 0.278212 }
 |