

|

|
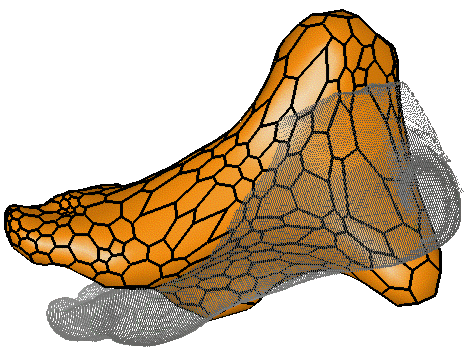
| (a) Initialization | (b) Rigid transformations |

|

|
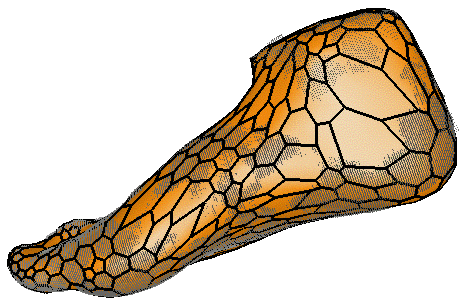
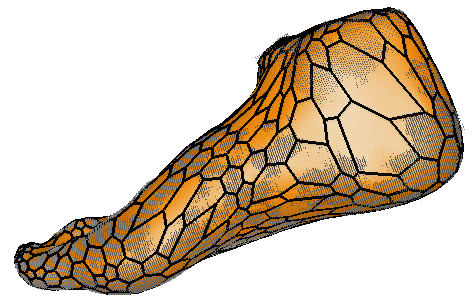
| (c) Hybrid deformations | (d) Local deformations |
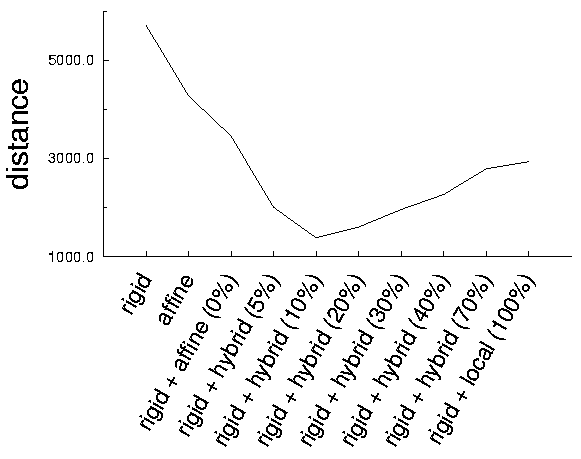
(e)Distance of the model to data after deformations
Consider unstructured data (a point set) of a foot and and a surface model (orange) we want to deform toward them (a). We can compute the distance between the model and the data after the model deformed as the sum of the distance of each vertex to its reference position given different deformation frameworks (e).
Figure (b) shows the result of the model rigid registration. No local deformations occured and the model remain far from the data. Let us then repeat the deformation experiment by increasing l each time. Figure (c) shows the deformation result for the hybrid framework (l = 10%) and figure (d) shows the result for the local framework. At first glance, those results appear to be very close but graph (e) shows that the distance first decrease as l increase up to 10% then increase again. This is due to a distorsion of the surface: when the model is not constrained enough (the locality coefficient l is too high), vertices of the surface can evolve toward the closest data point which is not the same geometric point. This means that a point at an extremity (such as a maximal curvature point for example) will not remain at this extremity throughout the deformation process. The resulting model does not preserve its geometric properties.