Simulation numérique du foie
 
MOSTRA - M3N  
 
Olivier ANTONELLI, Patrick le TALLEC, Marc THIRIET, Marina VIDRASCU

Rocquencourt Domaine de Voluceau
78153 Le Chesnay CEDEX

Objectifs

• Modèle précis (de référence) (PLT, MV)
  • élasticité non linéaire en grandes déformations
  • matériaux hyperélastiques (incompressibles)
  • éléments finis bien adaptés (Q2P1, P2P0)
  
  
• Méthode de résolution efficace (PLT, MV)
  • Newton avec continuation
  • Décomposition de domaines
  
  
• Résultats numériques (OA, PLT, MT, MV)
  • choix de la géométrie et des caractéristiques des matériaux
  • choix des conditions aux limites
  
  
• Comparer linéaire non-linéaire (OA)
  
• Qualité des résultats, Réalisme du simulateur

Model problem

Weak form of the equilibrium equations in a fixed reference configuration

$$\int_\Omega {\partial {\mathcal W} \over\partial F}(x, Id + \... ... \Green{f^{\Gamma}} \cdot v da, \forall v \in \mathbf(\Omega)$$

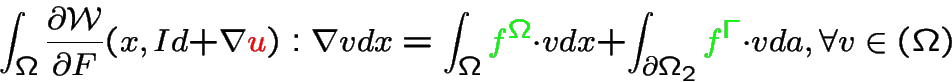
Hyper elastic constitutive law

$$T(x) = {\partial {\mathcal W} \over\partial F}(x, F), \quad F = Id + \nabla u,$$

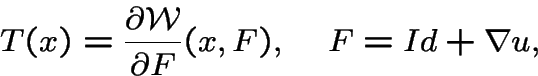
Total lagrangian formulation in abstract form

$${\mathcal F} (\Red{U}, f^\Omega, f^{\Gamma})= 0$$

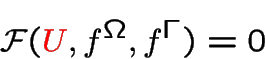
Highly nonlinear : specific form of the energy density

Constitutive energy of isotropic hyper-elastic materials

$$\begin{eqnarray*}&& {\mathcal W}(F) = \Green{C_1} (I_1 - 3) + \Green{C_2} (I_2 -... ...{a}(J^2-1)- (2 \Green{C_1} + 4 \Green{C_2} + 2 \Green{a}) logJ, \end{eqnarray*}$$

Newton algorithm

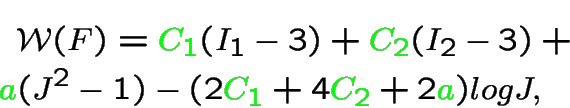
Iterative solution of linearized version

$${\partial {\mathcal F}(\Red{U^n}, f^\Omega, f^{\Gamma})\over... ...\Delta U + {\mathcal F}(\Red{U^n}, f^\Omega, f^{\Gamma}) =0,$$

$$\langle {\partial {\mathcal F}(U^n, f^\Omega, f^{\Gamma})\ov... ... {\mathcal W}} {\partial F^2}(x, Id + \nabla u) : \nabla v dx.$$

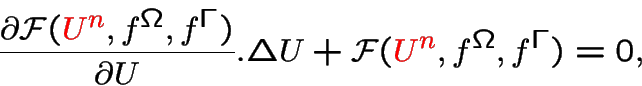
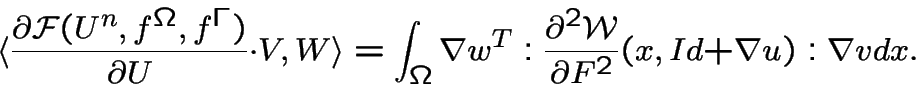
Converges fast if properly initialized

Continuation algorithm

Computes, by a Newton Euler algorithm with automatic time stepping the whole solution curve

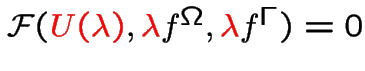${\mathcal F} (\Red{U(\lambda)}, \Red{\lambda} f^\Omega, \Red{\lambda} f^{\Gamma})= 0$ for $0 \leq \lambda \leq 1$

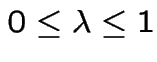
The major step is the solution of the large scale linear elasticity problem

• sparse
  
• ill conditioned

Deformation of the liver

Material characteristics :

Constitutive energy of isotropic hyper-elastic incompressible materials

E= 130 N/m² and $\nu = .5$

C₁=19.7 and C₂ =1.97

Geometrical characteristics :

Total mesh 6344 elements 9741 nodes split into 20 sub domains

elements	nodes	Matrix size	elements	nodes	Matrix size
323	636	1 127 016	319	647	1 039 542
315	622	916 572	311	608	1 080 312
316	603	686 862	316	589	936 768
323	618	1 074 600	315	626	739 410
314	599	996 900	313	633	894 060
330	639	1 104 210	317	623	1 103 370
331	640	1 285 176	312	611	971 466
312	627	956 358	316	629	1 037 382
313	630	1 207 746	313	671	845 664
318	604	1 011 792	314	605	1 132 494

Finite elements : P2-P0

Size of the whole matrix : 92 707 422

An idea about CPU time

1 Newton iteration on HP workstation : 8 hours for 1 domain 10 minutes for 20 subdomains with a cluster of workstations.

Perspectives

• Mieux exploiter le modèle numérique
  • conditions aux limites
    • noeuds à déplacement imposé
      
    • type : encastrement, simplement posé ...
      
    • post traitement
    
    

  • caractéristiques des matériaux

    utiliser des courbes expérimentales effort déplacement pour déterminer des valeurs de constantes des matériaux réalistes

  
  
• Affiner le modèle numérique : Ajouter un modèle surfacique de coque à forte résistance membranaire au modèle volumique sous-jacent avec des contraintes de déplacements égaux entre les deux.