Assume that exactly n documents reside in the
Web server which are requested at rates
r1 ![]() r2
r2 ![]()
![]()
![]() rn .
Assume that the sizes of the documents are identically distributed
random variables. Moreover, we shall assume that
the cache can hold a fixed number m of documents at any time
(note that this assumption clearly does not hold for
the ``smallest size'' caching policy).
Let Xi denote the index of the document of the i -th request,
and Yk,i the indicator function of whether document
k is in the cache at the i -th request.
We shall assume that {Xi}i is a sequence of independent and identically
distributed random variables.
Then, the empirical hit rate of caching policy
rn .
Assume that the sizes of the documents are identically distributed
random variables. Moreover, we shall assume that
the cache can hold a fixed number m of documents at any time
(note that this assumption clearly does not hold for
the ``smallest size'' caching policy).
Let Xi denote the index of the document of the i -th request,
and Yk,i the indicator function of whether document
k is in the cache at the i -th request.
We shall assume that {Xi}i is a sequence of independent and identically
distributed random variables.
Then, the empirical hit rate of caching policy ![]() , denoted by H
, denoted by H![]() ,
can be expressed as
,
can be expressed as
H![]() =
= ![]()
![]()
![]()
![]()
![]() 1(Xi = k)Yk,i.
1(Xi = k)Yk,i.
H![]() =
= ![]()
![]()
![]()
![]() E
E![]()
|
H | = |
| |
| = |
| ||
| = |
| ||
| = |
|
Note that
![]() qk(
qk(![]() ) =
) = ![]() E
E![]()
![]() m ,
and that for all k ,
0
m ,
and that for all k ,
0 ![]() qk(
qk(![]() )
) ![]() 1 .
Let rn + 1 = 0 . Then,
1 .
Let rn + 1 = 0 . Then,
|
H | = |
| |
| = |
| ||
| = |
| ||
|
|
| ||
| = |
|
Note that under the above assumptions (in particular, the documents have identical size), the ``request hit rate'' and the ``byte hit rate'' (see definitions below) coincide.
We assume now that the documents have different sizes, say bi bytes for document i . As in the previous case, we assume that ri is decreasingly ordered. Let B be the size of the cache. Then, the optimal static caching can be formulated as a 0-1 programming problem:
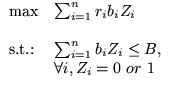
where Zi is the indicator function of whether document i is in the cache. The cost to be maximized is proportional to the byte hitrate
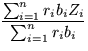 .
.
Let S denote the cost of the solution of this problem.
It is easy to see that such a problem is the
well-known knapsack problem, which is NP-hard in general.
Thus, in our implementation,
we consider an approximate solution resulting from relaxation.
Indeed, by relaxing the 0-1
constraint on Zi , i.e., by assuming that Zi is a real number
( Zi ![]() [0,1] ), we can easily see that an
optimal solution is
{Z1 = 1,Z2 = 1,,Zk = 1 ,
Zk + 1 = (B -
[0,1] ), we can easily see that an
optimal solution is
{Z1 = 1,Z2 = 1,,Zk = 1 ,
Zk + 1 = (B - ![]() bi)/bk),Zk + 2 = 0,,Zn = 0} ,
where
k = max {j
bi)/bk),Zk + 2 = 0,,Zn = 0} ,
where
k = max {j ![]() n|
n|![]() biZi
biZi ![]() B} .
B} .
Let Sr be the hitrate of the static caching
(using a cache whose size possibly exceeds B )
of documents
1,2,,k + 1 .
It is clear that
S ![]() Sr .
Sr .
Our approximate solution, denoted by Sa ,
is obtained by caching documents
1,2,,k and
some further documents after k that can be filled in the cache.
Again, it is clear that
Sa ![]() S
S ![]() Sr .
Sr .
This approximate solution is suboptimal. In practice, however, with the data of WWW documents access, this approximate solution Sa turns out to be very close to the upper bound Sr (the differences being smaller than 0.01% in our numerical experimentation). Therefore, we shall simply take the approximate solution as the optimal static solution. In section 4, the performance of this solution will be reported.