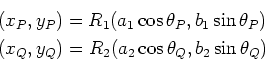
 Next: 24.3 Traitement de polynômes
Up: 24.2 Problème de CAO
Previous: 24.2.2 L'approche classique et
Next: 24.3 Traitement de polynômes
Up: 24.2 Problème de CAO
Previous: 24.2.2 L'approche classique et
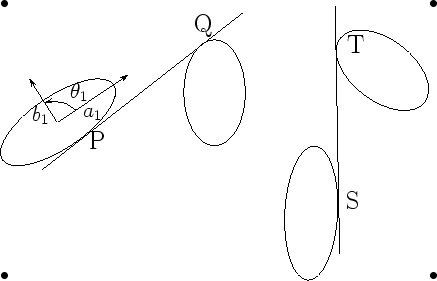
Le calcul des coordonnées des points d'intersection
n'est pas forcément nécessaire pour déterminer le
signe du déterminant
- rejeter les boîtes ne satisfaisant pas la contrainte de
choix sur les bi-tangentes
- couper les boîtes en évaluant le signe du
déterminant: si signe constant ne plus couper et stocker dans une
liste
 ou
ou 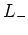 selon le signe
selon le signe
3 cas de figure:
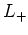 ou
ou 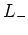 =
= 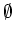 : signe du déterminant est
connue
: signe du déterminant est
connue
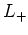 et
et 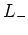
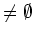 : couper les
boîtes de
: couper les
boîtes de 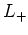 et
et  jusqu'à trouver celle où la
contrainte de choix est satisfaite ou que le cas 1- s'applique
jusqu'à trouver celle où la
contrainte de choix est satisfaite ou que le cas 1- s'applique
- une boîte tend vers un point sans que le signe du
déterminant soit constant: le signe du déterminant ne peut pas
être déterminé
Temps de calcul (modélisation algébrique): 0 à 40 ms
Que faire si le signe du déterminant est indéterminé ?
- passer en multi-précision: MPFI
- changer la modélisation: passer en polaire
donc
le changement de variables peut permettre de diminuer les erreurs
d'arrondis et d'arriver à statuer sur des cas non déterminés
dans la formulation algébrique

 Next: 24.3 Traitement de polynômes
Up: 24.2 Problème de CAO
Previous: 24.2.2 L'approche classique et
Jean-Pierre Merlet
Next: 24.3 Traitement de polynômes
Up: 24.2 Problème de CAO
Previous: 24.2.2 L'approche classique et
Jean-Pierre Merlet
2007-05-18