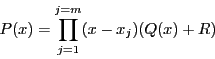Next: Parametric polynomial
Up: Simplification procedures
Previous: Simplification procedures
Contents
Deflation
The procedure DeflationUP will create a simplification procedure
based on a re-writting of the univariate polynomial 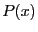 of degree
of degree 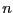 . Let us assume
that approximate roots
. Let us assume
that approximate roots
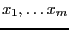 of the polynomial
of the polynomial 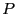 has been
found. Then the polynomial may be written as
has been
found. Then the polynomial may be written as
where 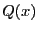 has degree
has degree 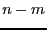 . In the generated simplification
procedure a C++ program will use the ALIAS_Nb_Solution
approximate roots
stored in the interval matrix ALIAS_Solution to compute safely
. In the generated simplification
procedure a C++ program will use the ALIAS_Nb_Solution
approximate roots
stored in the interval matrix ALIAS_Solution to compute safely
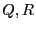 and will then use the above form of
and will then use the above form of 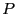 to compute the interval
evaluation of
to compute the interval
evaluation of 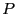 for the current box. If this evaluation does not
include 0, then the simplification procedure will return -1, allowing
the current box to be discarded.
for the current box. If this evaluation does not
include 0, then the simplification procedure will return -1, allowing
the current box to be discarded.
The syntax of this procedure is:
DeflationUP(Func,Vars,EvalProc,JevalProc,name)
where
- Func: the
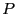 polynomial
polynomial
- Vars: the name of the polynomial variable
- EvalProc: the name of a C++ procedure in MakeF
format that will be used to
evaluate the polynomial. If GradientSolve or HessianSolve
are used as solving procedure this name is by default "F". Otherwise
the user may use its own procedure, for example by using MakeF.
- JevalProc: the name of a C++ procedure in MakeJ
format that will be used to
evaluate the derivative of the polynomial. If GradientSolve or HessianSolve
are used as solving procedure this name is by default "J". Otherwise
the user may use its own procedure, for example by using MakeJ.This procedure is used to compute accurately the approximate
roots of
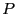 by using the Newton scheme with as initial guess the mid-point of the
global C++ variable
ALIAS_Solution until the residues are lower than `ALIAS/fepsilon`.
Alternatively you may specify "none" for JevalProc in
which case the mid-point of ALIAS_Solution will be used as
approximate solution
by using the Newton scheme with as initial guess the mid-point of the
global C++ variable
ALIAS_Solution until the residues are lower than `ALIAS/fepsilon`.
Alternatively you may specify "none" for JevalProc in
which case the mid-point of ALIAS_Solution will be used as
approximate solution
- name: the name of the simplification procedure that will
be written in the file name.C
To be used the coefficients of 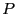 must be either real numeric or
intervals.
must be either real numeric or
intervals.




Next: Parametric polynomial
Up: Simplification procedures
Previous: Simplification procedures
Contents
Jean-Pierre Merlet
2012-12-20
![]() of degree
of degree ![]() . Let us assume
that approximate roots
. Let us assume
that approximate roots
![]() of the polynomial
of the polynomial ![]() has been
found. Then the polynomial may be written as
has been
found. Then the polynomial may be written as