



Next: The GlobalConsistencyTaylor procedure
Up: Filtering simplification procedures
Previous: The HullConsistencyTaylor procedure
Contents
This procedure is based on the interval evaluation of equations using
centered form with as centers two possible centers which may be
optimal (see the ALIAS C++ manual for the calculation of these
centers). The centered form uses the fact the interval evaluation of a
function 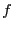 in the
in the 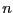 unknown
unknown
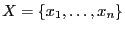 is included in
is included in
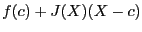 where
where 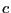 is point called the center. As mentioned
earlier two possible centers are calculated. Furthermore the
calculation of the product
is point called the center. As mentioned
earlier two possible centers are calculated. Furthermore the
calculation of the product 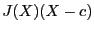 may involve several occurrences
of the same variables, that are not detected when computing the
product numerically. This procedure allows, as an option, to compute
symbolically the product and to re-arrange it in order to try to
reduce multiple occurrences.
may involve several occurrences
of the same variables, that are not detected when computing the
product numerically. This procedure allows, as an option, to compute
symbolically the product and to re-arrange it in order to try to
reduce multiple occurrences.
The syntax of this procedure is:
BiCenteredForm(func,funcproc,Jfuncproc,vars,custom,procname)
where
- func: a list of equations
- funcproc: the name of a procedure in MakeF format that computes the
interval evaluation of func
- Jfuncproc :the name of a procedure in MakeJ format that computes the
interval evaluation of the derivatives of func
- vars: a list of variable names
- custom: a string that indicate how funcproc and Jfuncproc are obtained.
- "none": the procedure will assume that funcproc
and Jfuncproc are
the procedures F and J that are generated by GradientSolve and HessianSolve
- "F": the procedure will assume that funcproc
is a customized procedure that, for example, has been generated by
MakeF
- "J": the procedure will assume that Jfuncproc is a customized procedure that, for example, has been generated by
MakeJ
- "FJ": the procedure will assume that funcproc and Jfuncproc are customized procedures
- procname: the name of the simplification procedure that
will be created in the file procname.C
In addition the procedure admits a 7th optional argument "prod". In that case the procedure will compute symbolically
the product 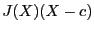 and re-arrange its terms. Both the numerical form
and the one resulting from the symbolic calculation will be used in
the simplification procedure.
and re-arrange its terms. Both the numerical form
and the one resulting from the symbolic calculation will be used in
the simplification procedure.




Next: The GlobalConsistencyTaylor procedure
Up: Filtering simplification procedures
Previous: The HullConsistencyTaylor procedure
Contents
Jean-Pierre Merlet
2012-12-20
![]() in the
in the ![]() unknown
unknown
![]() is included in
is included in
![]() where
where ![]() is point called the center. As mentioned
earlier two possible centers are calculated. Furthermore the
calculation of the product
is point called the center. As mentioned
earlier two possible centers are calculated. Furthermore the
calculation of the product ![]() may involve several occurrences
of the same variables, that are not detected when computing the
product numerically. This procedure allows, as an option, to compute
symbolically the product and to re-arrange it in order to try to
reduce multiple occurrences.
may involve several occurrences
of the same variables, that are not detected when computing the
product numerically. This procedure allows, as an option, to compute
symbolically the product and to re-arrange it in order to try to
reduce multiple occurrences.