



Next: Regularity of parametric matrices
Up: Linear algebra
Previous: Linear algebra
Contents
Let consider the family of linear systems defined by the matrix equality
where 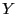 is a set of unknowns,
is a set of unknowns, 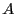 a square
a square 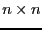 matrix whose
elements are functions of
matrix whose
elements are functions of 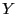 and
and 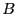 a
a 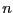 dimensional vector whose
elements are also functions of
dimensional vector whose
elements are also functions of 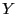 . The enclosure of the set of
solutions of this family of linear systems is a box that includes
the solution of all linear systems in the family.
. The enclosure of the set of
solutions of this family of linear systems is a box that includes
the solution of all linear systems in the family.
The enclosure can be computed using the LinearBound procedure
whose syntax is
LinearBound(A,B,Derivative,Vars,Init)
where:
- A is a square array whose elements are function of the unknowns
in Vars
- B is an array whose elements are function of the unknowns
in Vars
- Derivative is an integer. If set to 0 the procedure uses
the classical interval Gaussian elimination scheme to calculate the
enclosure. If set to 1 it will use an ALIAS specific version of the
Gaussian elimination scheme that uses the derivatives of the elements
of A, B to improve the enclosure calculation
- Vars: a list of unknowns names
- Init: a list of ranges for the unknowns
A typical example is:
with(ALIAS):
with(linalg):
A:=array([[x,y],[x,x]]):
B:=array([x,y]):
VAR:=[x,y]:
LinearBound(A,B,0,[x,y],[[3,4],[1,2]]);
LinearBound(A,B,1,[x,y],[[3,4],[1,2]]);
which returns the enclosure [[.76923076923077, 10], [-13, -.076923076923077]]
if Derivative is set to 0 and [[.91666666666667,
2.6666666666667], [-2, -.66666666666667]] if Derivative is set
to 1 (note that these values are computer dependent), the exact answer
being [[1.25,1.66666],[-1]].




Next: Regularity of parametric matrices
Up: Linear algebra
Previous: Linear algebra
Contents
Jean-Pierre Merlet
2012-12-20