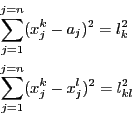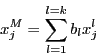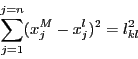Next: Specificity of the procedure
Up: Systems of distance equations
Previous: Systems of distance equations
Contents
The SolveDistance procedure
The SolveDistance procedure allows to solve systems of distance
equations. A distance equation describes that the distance between
m points in a n-dimensional space is given. The unknowns are the
n coordinates
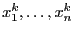 of the points. Hence a distance
equation may be written
as:
of the points. Hence a distance
equation may be written
as:
where 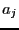 are numerical values.
Furthermore the algorithm allows for the use of virtual
points. The coordinates of a virtual point M are linear combination of
the coordinates of
are numerical values.
Furthermore the algorithm allows for the use of virtual
points. The coordinates of a virtual point M are linear combination of
the coordinates of 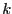 real points:
real points:
Hence a distance equation may also be written as:
The syntax of SolveDistance is:
SolveDistance(Func,Vars,Init)
The initial search domain for SolveDistance may be determined
using the Bound_Distance procedure.
Jean-Pierre Merlet
2012-12-20
![]() of the points. Hence a distance
equation may be written
as:
of the points. Hence a distance
equation may be written
as: