



Next: Systems of distance equations
Up: Specific solving procedures
Previous: Specific solving procedures
Contents
The SolveSimplex and SolveSimplexGradient
procedures
This procedure allows to solve systems that have algebraic terms in at
least at two equations. Each equation is transformed as the sum of a
linear part and a non linear part. The linear part is substituted into
a new variable that is submitted to a linear constraints. Then the
simplex method is used to improve the range for the unknowns.
The difference between the SolveSimplex and
SolveSimplexGradient procedure is that in the second case the
derivatives of the non linear parts of the equations are used to improve
their interval evaluation and hence the linear constraints used by
the simplex.
The following variables plays a role in these procedures:
- `ALIAS/diam_simplex`: the simplex will not be
applied if the width of the current box is lower than this value
(default value:0.1)
- `ALIAS/full_simplex`: if the value of this variable is
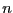 the simplex will be applied only
for searching the minimum and maximum of the first
the simplex will be applied only
for searching the minimum and maximum of the first 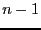 variables
when they are ordered by decreasing order of width. This is
probably the most important parameter to set: a compromise has to be
found between the gain of considering all variables and the
computation time of the simplex
variables
when they are ordered by decreasing order of width. This is
probably the most important parameter to set: a compromise has to be
found between the gain of considering all variables and the
computation time of the simplex
- `ALIAS/init_simplex_linear`: if some of the coefficients of the
linear part of the expressions have an identical value you may assign
this value to this variable so that a faster assignation of the
coefficients will be performed (available only for the parallel
version of these procedures). For example if a majority of the linear
coefficients are 2 setting `ALIAS/init_simplex_linear` to 2
implies that the C++ procedure that calculate the linear coefficients
will just compute the coefficients that are not equal to 2
- `ALIAS/min_diam_simplex`: the simplex will not be
applied if the width of the current box is larger than this value
(default value: 1.e7)
- `ALIAS/min_improve_simplex`: if the width of one
range of the box has been improved by a value larger than this
variable, then the simplex method will be repeated (default value: 0.1)
- `ALIAS/no_simplex`: if this parameter is set to 1 the
simplex will not be used. This may be interesting for the parallel
implementation where the computation involved by the simplex may be to
computer intensive for the master
- `ALIAS/simplex_expanded`: for the simplex method using the
gradient setting this flag to 1 indicates that the expression will be
expanded with respect to the lower bound of each variable (i.e.
the unknown
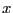 with lower bound
with lower bound 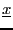 will be written as
will be written as
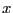 =
=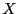 +
+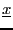 and the simplex method will use the variable
and the simplex method will use the variable
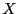 )
)




Next: Systems of distance equations
Up: Specific solving procedures
Previous: Specific solving procedures
Contents
Jean-Pierre Merlet
2012-12-20