Function evaluation

• when formulating your problem find the best compromise between the number of equations and their complexity. Having the lowest possible number of equations may not be the best if the equations are very complex
• remember that you are not stuck to algebraic equations
• first focus on the problem at hand, not on the equations (see the example in the next section and the example in section 13.2.3.1)
• give the equations from the simplest to the more complex
• if you are using methods involving the gradient and have equations that are similar in the number of terms give first the equations that may have a gradient with a constant sign
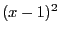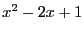• try to factor our most of the term (e.g. $(x-1)^2$ will in general be better than $x^2-2x+1$). ALIAS-Maple will try to do this job for you but any help is welcome!
• try to normalize your equation and variable