



Next: The Bound_Distance procedure
Up: Utilities procedures of ALIAS-Maple
Previous: Transformation of an expression:
Contents
Newton scheme
We have a specific Maple implementation of the Newton scheme
which is mostly
be intended to be used in conjunction with the result of the solving
algorithms of ALIAS-C++.
The main purpose of this procedure is to allow to refine the accuracy
of the result provided by the solving procedures of ALIAS-C++ which
have an accuracy of double. It will allow to calculate the roots
of a system with an accuracy that is specified in term of number of
digits. For example when specifying an accuracy of 200 digits the
result provided by this procedure (when it succeeded) will be a number
with 200 digits, the
last digit being guaranteed to be the correct digit for the
solution.
Newton(Func,Vars,Init,Maxiter,Acc)
where
- Func: a list with the system of equations to be solved
(which must be
square)
- Vars: a list with the name of the unknowns
- Init: a list for the initial guess. This list may be
either an element
of the list returned by the solving procedure of ALIAS (i.e. with
2 elements for each variable) or a list with one element for each
variable
- Maxiter: maximum number of iteration allowed for the
scheme
- Acc: accuracy for the solution: the Acc-th bit is guaranteed to
be exact
This procedure returns:
- -4: number of Init element not compatible with the number
of elements in Vars
- -2: not a square system
- -3: singular jacobian matrix
- -1: more than MaxIter iterations
- 1: success
and the estimation of the solution in ALIAS_Newton.
Clearly this procedure may fail to return a correct result in some
cases: for example if the correct result of an univariate equation is
2 it may happen that the numerical Newton scheme always converge
to 1.999999999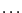 .
.




Next: The Bound_Distance procedure
Up: Utilities procedures of ALIAS-Maple
Previous: Transformation of an expression:
Contents
Jean-Pierre Merlet
2012-12-20
![]() .
.