



Next: Example
Up: Implementation without gradient
Previous: The CoeffLinear procedure
Contents
In some case it may be interesting to consider an expansion of the
function around a given point. For example consider the term
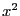 with
with 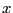 in the range [1,2]: in the simplex method the range
[1,4], for this term
will be added to the non linear part of the equation. But if we
substitute the unknown
in the range [1,2]: in the simplex method the range
[1,4], for this term
will be added to the non linear part of the equation. But if we
substitute the unknown 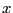 by a new unknown
by a new unknown 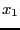 such that
such that 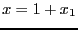 (hence the range for
(hence the range for 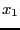 will be [0,1])
we will get
will be [0,1])
we will get
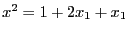 we will get an additional linear term
(
we will get an additional linear term
(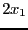 ) while the non linear part will be
) while the non linear part will be 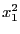 with the range
[0,1]. For each variable
with the range
[0,1]. For each variable 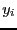 in the range
in the range
![$[\underline{y_i},\overline{y_i}]$](img378.png) we may define a new variable
we may define a new variable
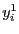 such that
such that
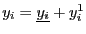 where
where 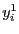 has the
range
has the
range
![$[0,\overline{y_i}-\underline{y_i}]$](img381.png) . We may then write the non
linear and linear procedures for the unknowns
. We may then write the non
linear and linear procedures for the unknowns 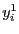 but it necessary
to notify the simplex procedure that such an expansion is used. This
is done by setting the flag
ALIAS_Simplex_Expanded to 1 (this possibility is available
only for the simplex method using the gradient).
but it necessary
to notify the simplex procedure that such an expansion is used. This
is done by setting the flag
ALIAS_Simplex_Expanded to 1 (this possibility is available
only for the simplex method using the gradient).
You may also prohibit the use of the simplex method in the procedure
(for example to use it only in your own simplification procedure) by
setting the flag ALIAS_DONT_USE_SIMPLEX to 1.




Next: Example
Up: Implementation without gradient
Previous: The CoeffLinear procedure
Contents
Jean-Pierre Merlet
2012-12-20