



Next: Hessian procedure
Up: General purpose solving algorithm
Previous: Single bisection mode
Contents
The generic implementation of this solving procedure is:
int Solve_General_JH_Interval(int Dimension_Var,int Dimension_Eq,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Order,
int Iteration,
int Stop_First_Sol,
double Accuracy_Variable,
double Accuracy,
INTERVAL_MATRIX & Solution,
INTEGER_VECTOR & Is_Kanto,
int Apply_Kanto,
int Nb_Max_Solution,INTERVAL_MATRIX &Grad_Init,
int (* Simp_Proc)(INTERVAL_VECTOR &),
int (* Local_Newton)(int Dimension,int Dimension_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Input,double Accuracy,int Max_Iter, VECTOR &Residu,INTERVAL_VECTOR &In))
the arguments being:
- m: number of unknowns
- n: number of functions, see the note 2.3.4.1
- Type_Eq: type of the functions, see the note 2.3.4.2
- IntervalFunction: a function which return the interval
vector evaluation of the functions, see the
note 2.3.4.3. Remember that if you have equations and
inequalities in the system you must first define the equations and
then the inequalities.
- IntervalGradient: a function which return
the interval matrix of the
jacobian of the functions, see the note 2.4.2.2
- IntervalHessian: a function which return
the interval matrix of the
Hessian of the functions, see the note 2.5.2.1
- TheDomain: box in which we are looking for
solution of the system. A copy of the search domain is available in
the global variable ALIAS_Init_Domain
- Order: the type of order which is used to store the
intervals created during the bisection process. This order may be
either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of
boxes which may be
stored. See the note 2.5.2.2
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has
been found
- 2: the algorithm will stop as soon as Nb solutions
have been found
- epsilon: the maximal width of the box, see the
note 2.3.4.6
- epsilonf: the maximal width of the function intervals, see the
note 2.3.4.6
- Solution: an interval matrix of size (Nb,m)
which will contained the solution intervals. Each solution may be:
- a set of intervals with the associated flag IsKanto to 0:
- a set of intervals with the associated flag IsKanto to 1: there is an unique solution in the set and Newton
method will converge toward this solution
- a set of intervals reduced to a point with the
associated flag IsKanto to 0: this point is a solution which has been obtained with Krawczyk
method (see 2.10). The accuracy of this solution may be improved
by using the point as starting point for Krawczyk
method and decreasing the accuracy epsilonf
- IsKanto: an integer vector of dimension Nb. A value
of 1 for IsKanto(i)
indicate that applying Newton method (see section 2.9)
with as estimate the center of the solution intervals Solution(i) will
converge toward the unique solution which lie within the
solution intervals Solution(i)
- ApplyKanto: an integer which indicate at which
level we use Kantorovitch theorem. If 1 we use Kantorovitch theorem
(see section 3.1.2 and the mathematical
background) to determine the solution. A consequence is
that the solution interval may have a width larger than epsilon. If 0 we use Kantorovitch theorem just to separate the
solutions: the solution interval will have a width epsilon.
If 2 we will apply Newton method for every box which has not been
eliminated during the bisection process but we will consider the
result a solution only if it lie within the box. The maximal number of
iteration is determined by the global variable Max_Iter_Newton_JH_Interval (by default
100).
In that case we may miss solutions if they are lying inside the same box.
- Nb: the maximal number of solution which will be returned
by the algorithm
- GM: an interval matrix which give a-priori information on
the values of the derivatives of the function. GM(i,j) is the
interval value of the derivative of function i with respect to
variable j
- Simp_Proc: a user-supplied procedure that take as input
the current box and proceed to some further reduction of
the width of the box or even determine that there is no
solution for this box, in which case it should return
-1 (see note 2.3.3).
Remember that you may use the 3B method to improve the efficiency of
this algorithm (see section 2.3.2).
- Local_Newton: a Newton scheme that is used when Apply_Kanto is set to 2. When omitted the algorithm will use the
ALIAS Newton procedure (see section 2.9).
Note that the following arguments may be omitted:
- Type_Eq: in that case all the functions will supposed to be
equations.
- GM: in that case all the derivatives will
supposed to be unknown
- Simp_Proc: no simplification procedure is provided by the
user
- Local_Newton
The following variables play also a role in the computation:
- ALIAS_Store_Gradient: if not 0 the gradient matrix of
each box will be stored together with the boxes.
Must be set to 0 for large problem
(default value: 1)
- ALIAS_Diam_Max_Gradient: if the maximal width of the
ranges in a box is lower than this value, then the
gradient will be used to perform the interval evaluation of the
functions (default value: 1.e10)
- ALIAS_Diam_Max_Kraw: if the maximal width of the
ranges in a box is lower than this value, then the
Krawczyk operator will be used to determine if there is a unique
solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the
ranges in a box is lower than this value, then the
interval Newton method will be used either to try to reduce
the width of the box or to to ensure that there is no solution of the
system in the box (default value: 1.e10)
- ALIAS_Always_Use_Inflation: if ApplyKanto is set
to 1 we get for each solution a box
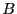 which contains only one
solution. If this flag is set to 1 we compute the solution using
Newton and then we use an inflation procedure that try to determine a
box
which contains only one
solution. If this flag is set to 1 we compute the solution using
Newton and then we use an inflation procedure that try to determine a
box 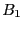 which is larger than
which is larger than 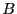 and contains also only one solution
and contains also only one solution
- ALIAS_Eps_Inflation: the inflation algorithm will try to
increase the width of the box
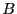 by at least this value
by at least this value
- ALIAS_Sing_Determinant: if the determinant of the
jacobian matrix of the system is lower than this value, then the
system is supposed to be singular
- ALIAS_Diam_Sing: for a value
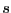 of this
parameter if there is singular solution in the
system, then the algorithm will not look for solution of the system in
a box of width 2
of this
parameter if there is singular solution in the
system, then the algorithm will not look for solution of the system in
a box of width 2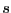 around the singular solution (default value: 0)
around the singular solution (default value: 0)
- ALIAS_Use_Grad_Equation: if this integer array has a
size of n the derivatives of equation
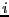 will be used to
evaluate the i-th equation only if ALIAS_Use_Grad_Equation[i]
is not 0
will be used to
evaluate the i-th equation only if ALIAS_Use_Grad_Equation[i]
is not 0
- ALIAS_No_Hessian_Evaluation: if set to 0 we will not
use the Hessian to sharpen the interval evaluation of the Gradient
when performing the interval evaluation of the equations. This may be
useful if its known that the interval evaluation of the elements of
the hessian will
have always a constant sign
Subsections




Next: Hessian procedure
Up: General purpose solving algorithm
Previous: Single bisection mode
Contents
Jean-Pierre Merlet
2012-12-20