



Next: Example 4
Up: Examples
Previous: Example 2
Contents
Example 3
This example is derived from example 2. We notice that in the three
equations of example 2 the second degree terms of 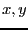 are for all
functions
are for all
functions 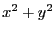 . Thus by subtracting the first function to
the second and third we get a linear system in
. Thus by subtracting the first function to
the second and third we get a linear system in 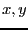 . This system is
solved and the value of
. This system is
solved and the value of 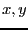 are substituted in the first
function. We get thus a system of one equation in the unknown
are substituted in the first
function. We get thus a system of one equation in the unknown
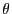 (see section 15.1.2).
The roots of this equation are 0,-0.8067834380. The test program is
Test_Solve_Gradient_General2.
The IntervalGradient function is written as:
(see section 15.1.2).
The roots of this equation are 0,-0.8067834380. The test program is
Test_Solve_Gradient_General2.
The IntervalGradient function is written as:
INTERVAL_MATRIX IntervalGradient (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_MATRIX Grad(1,1);
Grad(1,1)=-3788.0+(2692.0+(7576.0-4800.0*Cos(in(1)))*Cos(in(1)))*Cos(in(1))+(
25912.0+(-39320.0+14520.0*Cos(in(1)))*Cos(in(1)))*Sin(in(1));
return Grad;
}
With epsilonf=0 and epsilon=0.001
we get the solution by using 8 boxes:
for whatever order.
The solution intervals contain the roots of the
equation.
If we use epsilon=0 and epsilonf=0.1 we get by
using 8 boxes:
Here we get a unique solution and a range solution. But we notice that
the solution 0 is exactly the middle point of the test domain: Moore
test will fail as 0 will always be an end-point of the range. If we
break the symmetry of the test domain we will get exactly both solutions.




Next: Example 4
Up: Examples
Previous: Example 2
Contents
Jean-Pierre Merlet
2012-12-20