Evaluation procedure using the Jacobian

A better evaluation of the function intervals than the IntervalFunction can be obtained using the Jacobian matrix. A specific procedure can be used to obtain this evaluation:

 
INTERVAL_VECTOR Compute_Interval_Function_Gradient(int m,int n, 
        INTEGER_VECTOR &Type_Eq,
        INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &), 
        INTERVAL_MATRIX (* IntervalGradient)(int, int, INTERVAL_VECTOR &), 
        INTERVAL_VECTOR & Input, int Exact,
        INTEGER_VECTOR &AG,INTEGER_MATRIX &AR)

This procedure computes the function intervals for the box Input.

• Type_Eq is an integer array whose Dimension_Eq elements indicates the nature of the functions: -1 for inequality 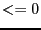$<=0$, 0 for equation, 1 for inequality 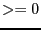$>=0$, -2 for a function to be minimized, 2 for a function to be maximized and 10 for a function to be both minimized and maximized (note that for an optimization problem the function that has to be minimized must be the last function in the list of function).
• the integer Exact should be put to 1 as for a value of 0 the procedure stop the evaluation of each box as soon as the lower bound of the interval is negative and the upper bound positive.
• AG is an integer vector of size m x n which indicates if the sign of some derivatives are already known (the elements should then have the values -1, 0 or 1) or not (the value must then be 2)
• AR is a return matrix with the sign of the derivatives for Input

The parameters Type_Eq, AG, AR may be omitted. This procedure uses the derivatives for improving the interval evaluation of the functions in two different ways:

• by taking into account of the monotonicity of the functions
• by using an interval evaluation of the functions based on their Taylor expansion: it is therefore necessary to evaluate rightly the derivatives of the functions

The best evaluation of the l-th equation may be computed with

 
INTERVAL Compute_Interval_Function_Gradient_Line(int l,int Dim_Var,
int Dimension_Eq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &), 
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
INTERVAL_VECTOR &Input,int Exact,INTEGER_VECTOR &AG)