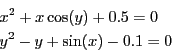Next: Practical implementation
Up: The generic analyzer
Previous: The generic analyzer
Contents
The purpose of the generic analyzer is to try to refine a box
and to propose smaller sub-intervals which may contain real roots
of the system of equations (which may be algebraic or not). Two types
of tools are used for that
purpose:
- as soon as one of the equation in the system is algebraic in at
least one of the unknowns then the tools described for determining
ranges on the roots of an univariate polynomial with interval
coefficients are used recursively
- otherwise Kantorovitch theorem is used (if you have
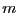 equations and
equations and  unknowns with
unknowns with 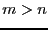 , then this theorem is applied
only for the first
, then this theorem is applied
only for the first  equations)
equations)
More precisely consider the system in two unknowns:
In a first step the first equation is considered: it will be
considered as a polynomial in 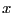 with the interval coefficients
with the interval coefficients
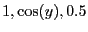 . Bounds on the real roots of this polynomial will be
computed and the range on
. Bounds on the real roots of this polynomial will be
computed and the range on 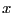 will be updated if necessary. Then the
second equation will be considered as a polynomial in
will be updated if necessary. Then the
second equation will be considered as a polynomial in 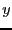 with
interval coefficients
with
interval coefficients
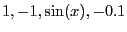 Bounds on the real roots of
this polynomial will be
computed and the range on
Bounds on the real roots of
this polynomial will be
computed and the range on 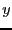 will be updated if necessary. After
these two steps if a range has been improved we will reiterate the
process until no further improvement is obtained.
will be updated if necessary. After
these two steps if a range has been improved we will reiterate the
process until no further improvement is obtained.
We will then try to improve the obtained ranges by using
Kantorovitch theorem. We consider the middle point of the ranges and test if
Kantorovitch is able to determine a ball centered at this point for
which Newton method will converge toward the unique solution in the
ball. If the answer is positive we will use Newton with as starting
point the center of the ball: the result, a point, is stored as one of
the result ranges. The intersection of the ball with the initial range
will then be computed and if non empty will be stored for further
processing.
We may indeed perform an in-depth analysis. The previous process is
applied on the initial range and will lead to a set of ranges
(possibly to the same ranges than the initial one); we may then
bisect the obtained ranges and reiterate the process on the resulting
ranges, discarding those for which the interval evaluation for at
least one of the
equations does not include 0. We define
a depth level for the algorithm as the number of bisection steps
that will be used in the process (a depth 0 means that no bisection
will be done).




Next: Practical implementation
Up: The generic analyzer
Previous: The generic analyzer
Contents
Jean-Pierre Merlet
2012-12-20