



Next: Using the ALIAS parser
Up: Parser, Generic Solver and
Previous: Parser, Generic Solver and
Contents
The ALIAS parser
As it has been seen in the previous chapters the interval evaluation
of an equation is highly dependent upon its formulation (for example
the evaluation of 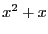 may be quite different from the evaluation
of
may be quite different from the evaluation
of 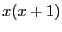 for the same range on
for the same range on 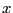 ).
For testing purposes it may therefore be interesting to
change the formulation of an equation (for example by using MAPLE),
write its analytical form in a file and test what will be the interval
evaluation of this equation in this analytical form: this is one
objective of the ALIAS
parser. Basically this parser takes as input:
).
For testing purposes it may therefore be interesting to
change the formulation of an equation (for example by using MAPLE),
write its analytical form in a file and test what will be the interval
evaluation of this equation in this analytical form: this is one
objective of the ALIAS
parser. Basically this parser takes as input:
- a file, called
a
formula file, in which is written the
analytical form of the equation
- name and ranges for the variables
and will then produces as output the interval evaluation of the equations.
In the formula file you may indicate an arbitrary
number of equations, each of them
being prefixed by eq=. For example
eq=(y^2-1)*z+(2*y*t-2)*x
eq=2+(-10*t+(-10+2*y*t)*y)*y+((4+4*y^2)*z+(4+4*y*t-x*z)*x)*x
eq=(2*y*t-2)*z+(t^2-1)*x
eq=2+(4*x+(4-x*z)*z)*z+((-10+4*z^2)*y+(-10+4*x*z+2*y*t)*t)*t
is a valid formula file in
parser format. There is however a limitation on the number
of unknowns which cannot exceed 200.
Note that the variable names in a formula file may be any name
composed with lower and upper
cases, integer numbers and underscore, with the constraint
that the first character should be a letter.
Note also that a MAPLE library
enables to produce a formula file directly from MAPLE equations (see
section 12.3).
The parser may handle almost any complex
analytical equation based on the most classical mathematical functions,
using MAPLE notation.
Currently you may use the following operators:
- arithmetic operator: "+","-","/","*"," " or "**" (power)
- trigonometric and inverse trigonometric functions: sin,
cos, tan, arcsin, arccos, arctan (which
may be used with the syntax arctan(x) or arctan(y,x))
- hyperbolic functions: sinh, cosh, tanh, arcsinh, arccosh, arctanh
- mathematical functions: abs (absolute value), log,
log10, exp, sqrt
- integer functions: ceil (returns an interval which bounds
are the smallest integer greater than or equal to each bound of the
box, floor (returns an interval which bounds
are the greatest integer less than or equal to each bound of the box),
round (returns an interval which bounds
are the nearest integer of each bound of the box)
Beside these functions we have added a few more operators:
The parser may also handle intervals. For example you may evaluate an
equation in which some coefficients are intervals. In the equation
these coefficients should be indicated using the MAPLE notation as in
the following example:
INTERVAL(0.1 .. sin(1))
Subsections




Next: Using the ALIAS parser
Up: Parser, Generic Solver and
Previous: Parser, Generic Solver and
Contents
Jean-Pierre Merlet
2012-12-20