



Next: Full continuation procedure
Up: Implementation
Previous: Certified Newton
Contents
This procedure takes as input a set of  solutions of the system and
will return points on the
solutions of the system and
will return points on the  branches. The branches will be followed
until a given value for the parameter is reached or if Kantorovitch
theorem is no more satisfied for some value of the parameter.
It is implemented as:
branches. The branches will be followed
until a given value for the parameter is reached or if Kantorovitch
theorem is no more satisfied for some value of the parameter.
It is implemented as:
int ALIAS_Start_Continuation(int m,int n,int NUM,
INTERVAL_MATRIX &Solutions,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalHessian)(int,int,INTERVAL_VECTOR &),
double epsilon,double epsilonf,
double *z,double delta,double mindelta,
INTERVAL &Rangez,
int sens,
MATRIX &BRANCH,int *NBBRANCH)
the arguments being:
- m: number of unknowns
- n: number of equations
- NUM: the number of solutions of the system for the current
value of the parameter z
- Solutions: the solutions of the system for the current
value of the parameter z
- IntervalFunction: a function which return the interval
vector evaluation of the equations, see
note 2.3.4.3.
- IntervalGradient: a function which return
the interval matrix of the
jacobian of the equations, see note 2.4.2.2
- IntervalHessian: a function which return
the interval matrix of the
Hessian of the equations, see note 2.5.2.1
- epsilon: the maximal width of the box, see the
note 2.3.4.6. If all the variable ranges have a width lower than
this value and the interval evaluation of the equations contains all
0, then the set of ranges is considered to be a solution. But they
will be not considered as a valid solution as they will not satisfy
Kantorovitch theorem. Hence you must put here a very small value
- epsilonf: the maximal width of the equation intervals, see the
note 2.3.4.6. This value will be used by the iterative Newton
scheme to stop the iteration.
- z: the parameter of the system
- delta: if
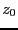 is the first value of the parameter such
that the system has solutions, then we will store in BRANCH the
solutions for
is the first value of the parameter such
that the system has solutions, then we will store in BRANCH the
solutions for 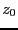 +delta,
+delta, 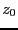 +2delta,...
+2delta,...
- mindelta: if the algorithm is unable to find a
Kantorovitch solution for the parameter value z+mindelta while a
solution has been found for z, then the algorithm will assume
that we are close to a singular point. Hence mindelta should
have a small value
- Rangez: the range for the parameter z
- sens: either 1 or -1. If 1 the branch will be computed for
increasing values of z, if -1 for decreasing values of z. This parameter should be chosen according to the largest number of
solutions of the system for the lower and upper value of z
- BRANCH: the procedure will return an array of NBBRANCH lines and m+2 columns, which describe the points of
the branch. In a line the first m+1 elements are the coordinates
of the point and the m+2 elements is the number of the branch to
which belong this point. The points are not ordered with respect to
the branch number. The algorithm will take care of resizing BRANCH as needed, hence there is no need to give dimension for this parameter
- NBBRANCH: the total number of points in the array BRANCH.
The return code is:
- 1: the branches have been successfully determined
- -1, -2: the algorithm has failed to find a Kantorovitch solution
for the current value of the parameter
- -3: failure in Newton method (should not occur)
- -10: for the current value of the parameter the jacobian is
singular
- -20: sens is not 1 or -1
- -30: delta or mindelta is negative
Even for a negative return code the points in BRANCH are valid:
the procedure will return the points that have computed on the  branches but is simply not able
to determine the location of new branches that may have appeared.
branches but is simply not able
to determine the location of new branches that may have appeared.




Next: Full continuation procedure
Up: Implementation
Previous: Certified Newton
Contents
Jean-Pierre Merlet
2012-12-20
![]() solutions of the system and
will return points on the
solutions of the system and
will return points on the ![]() branches. The branches will be followed
until a given value for the parameter is reached or if Kantorovitch
theorem is no more satisfied for some value of the parameter.
It is implemented as:
branches. The branches will be followed
until a given value for the parameter is reached or if Kantorovitch
theorem is no more satisfied for some value of the parameter.
It is implemented as: