



Next: Implementation
Up: Continuation 1D
Previous: Continuation 1D
Contents
Let consider a system of  equations in
equations in 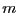 unknowns
unknowns
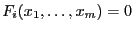 and assume that
and assume that 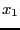 may vary in the range
may vary in the range
![$[\underline{x_1},\overline{x_1}]$](img765.png) and that it is considered as the
parameter of this
system. Using the solving algorithms of
ALIAS (or any other
method) we are able to determine the real roots of this system, if any, for a
given value of the parameter, for example for
and that it is considered as the
parameter of this
system. Using the solving algorithms of
ALIAS (or any other
method) we are able to determine the real roots of this system, if any, for a
given value of the parameter, for example for
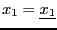 . Let
assume that we have found
. Let
assume that we have found 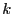 real roots
real roots
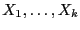 . Assume now
that we change the value of
. Assume now
that we change the value of 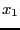 to
to
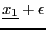 . Using
Kantorovitch theorem (see section 3.1.2)
we are able to determine if Newton method with as
initial estimate
. Using
Kantorovitch theorem (see section 3.1.2)
we are able to determine if Newton method with as
initial estimate 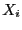 will converge toward a solution of the new
system and the radius
of convergence
will converge toward a solution of the new
system and the radius
of convergence 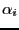 such that the solution is unique in the ball
such that the solution is unique in the ball
![$B_i =[X_i-\alpha_i, X_i+\alpha_i]$](img771.png) (alternatively we may also use
Moore theorem, see section 2.10).
If this is the case and if the
intersection of the
(alternatively we may also use
Moore theorem, see section 2.10).
If this is the case and if the
intersection of the 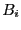 is empty, then we are able to compute in a
certified way the new
is empty, then we are able to compute in a
certified way the new 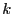 solutions of the new system. Otherwise we
will repeat the procedure with a smaller value for
solutions of the new system. Otherwise we
will repeat the procedure with a smaller value for 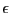 until
the method succeed. A failure case will be when the system become
singular at a point (for example when 2 branches are collapsing). If
this happen we will change the value of
until
the method succeed. A failure case will be when the system become
singular at a point (for example when 2 branches are collapsing). If
this happen we will change the value of 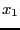 until we find a new set of solutions
which satisfy Kantorovitch theorem and start again the process.
until we find a new set of solutions
which satisfy Kantorovitch theorem and start again the process.
This method enable to follow all the branches for which initial points have
been found when solving the initial system. We may then store these
points in an array, for example at regular step for the value
of the parameter.
By default we use Kantorovitch theorem to follow the branches but by
setting the global variable
ALIAS_Use_Kraw_Continuation
to 1 we will use Moore test.




Next: Implementation
Up: Continuation 1D
Previous: Continuation 1D
Contents
Jean-Pierre Merlet
2012-12-20