



Next: Return code
Up: Implementation
Previous: Implementation
Contents
The optimization
method is implemented as:
int Minimize_Maximize(int m,int n,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Iteration,int Order,
double epsilon,double epsilonf,double epsilone,
int Func_Has_Interval,
INTERVAL Optimum,
INTERVAL_MATRIX & Solution,
int (* Simp_Proc)(INTERVAL_VECTOR &));
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- Type_Eq: type of the equations:
- Type_Eq(i)=-1 if equation i is a constraint
equation of type
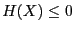
- Type_Eq(i)=0 if equation i is a constraint
equation of type
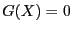
- Type_Eq(i)=1 if equation i is a constraint
equation of type
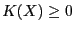
- Type_Eq(i)=-2 if equation i is the optimum
function to be minimized
- Type_Eq(i)=2 if equation i is the optimum
function to be maximized
- Type_Eq(i)=10 if equation i is the optimum
function for which is sought the minimum and maximum
- IntervalFunction: a function which return the interval
vector evaluation of the equations, see the note 2.3.4.3. This
function must be written in a similar manner than for the general
solving procedures.
Note also that a convenient way to write the IntervalFunction
procedure is to use the possibilities offered by the ALIAS-Maple
(see the ALIAS-Maple manual).
- TheDomain: box in which we are looking for
the extremum of the optimum function
- Iteration: the number of boxes that may be
stored
- Order: a flag describing which order is used to store the
new boxes, see the note 8.3.4
- epsilon: the maximal width of the solution intervals but
not used. Should be set to 0.
- epsilonf: the maximal error for the equality
constraints. If the
problem has constraint of type
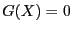 then a solution will verify
then a solution will verify
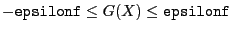
- epsilone: the maximal error on the extremum value.
If the extremum of the function is
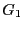 and the procedure
returns the value
and the procedure
returns the value 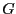 , then a minimum will verify
, then a minimum will verify
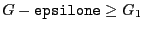 and a maximum
and a maximum
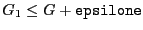 .
.
- Func_Has_Interval: 1 if the optimum function has
interval coefficients, 0 otherwise
- Optimum: an interval which contain the extremum value of
the optimum function
- Solution: an interval matrix of size at least (2,m)
which will contained the values of
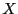 for which the extremum are
obtained
for which the extremum are
obtained
- Simp_Proc: an optional parameter which is a
simplification
procedure that may be provided by the user. It takes as input a box
 and may:
and may:
- either returns in
 a box with lower width than the initial
a box with lower width than the initial
 and a return code 0 or 1
and a return code 0 or 1
- or indicates that there is no solution to the
optimization problem in the current box, in which case the procedure
returns -1
An often efficient simplification procedure is the 2B method (see
section 2.17) that may be automatically generated by the
HullIConsistency procedure of ALIAS-Maple
Thus to minimize a function you have to set its Type_Eq to -2,
to maximize it to set its Type_Eq to 2, while if you are
looking for both a minimum and a maximum Type_Eq should be set
to 10.
Remember that you may use the 3B method to improve the efficiency of
this algorithm (see section 2.3.2) if you have constraint equations.
In some cases it may be interesting to determine if the minimum and
maximum have same sign. This may be done by setting the flag
ALIAS_Stop_Sign_Extremum either to:
- 1: the procedure will return immediately as soon as it is proven
that the extremum will have opposite sign i.e. as soon as two points
lead to opposite value for the function. But if the extremum have
identical sign the minimum and maximum will be computed up to the
accuracy epsilone
- 2: the procedure will return immediately as soon as it is proven
that the extremum will have opposite sign i.e. as soon as two points
lead to opposite value for the function. If the extremum have same
sign the values returned by the procedure are not the minimum and
maximum of the function
With the flag set to 2 the detection that the extremum will have
opposite sign is faster.
Subsections




Next: Return code
Up: Implementation
Previous: Implementation
Contents
Jean-Pierre Merlet
2012-12-20
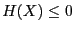
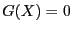
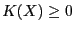
 a box with lower width than the initial
a box with lower width than the initial
 and a return code 0 or 1
and a return code 0 or 1