



Next: Regularity of parametric interval
Up: Solving systems of linear
Previous: Mathematical background
Contents
The simplest Gaussian elimination scheme is implemented as:
int Gauss_Elimination(INTERVAL_MATRIX &Ain,
INTERVAL_VECTOR &b,INTERVAL_VECTOR &bout)
where
- Ain: the A interval matrix
- b: the b interval vector
- bout: the enclosure of the set of solutions
The procedure returns 1 if it has succeeded in finding the enclosure,
0 otherwise (one of the interval pivot in the Gaussian scheme includes
0).
This computation for the initial system and a pre-conditioned system
has been implemented in the procedure:
int Gauss_Elimination_Derivative(MATRIX &Cond,INTERVAL_MATRIX &Ain,
INTERVAL_MATRIX &ACondin,
const INTERVAL_VECTOR bin,
const INTERVAL_VECTOR bCondin,
INTERVAL_VECTOR &bout,
INTERVAL_VECTOR & Param,
INTERVAL_VECTOR (* Func)(int l1, int l2, INTERVAL_VECTOR & v_IS),
INTERVAL_MATRIX (* JFunc)(int l1, int l2, INTERVAL_VECTOR & v_IS),
INTERVAL_VECTOR (* bFunc)(int l1, int l2, INTERVAL_VECTOR & v_IS),
INTERVAL_MATRIX (* JbFunc)(int l1, int l2, INTERVAL_VECTOR & v_IS))
where
- Cond: the pre-conditioning matrix. If all the elements of
Cond are 0 the procedure will implement the Gauss elimination
scheme only on the initial system
- Ain: the interval evaluation of the
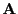 matrix
matrix
- ACondin: the interval evaluation of the Cond
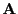 matrix
matrix
- bin: the interval evaluation of
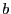
- bCondin: the interval evaluation of Cond
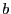
- bout: the enclosure of the interval linear system
- Param: the ranges for
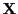
- Func: a procedure that computes the interval evaluation of
the elements of
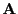 . These elements are stored rows by rows in
an
. These elements are stored rows by rows in
an 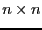 interval vector (see the note 2.3.4.3)
interval vector (see the note 2.3.4.3)
- Jfunc: a procedure that computes the interval evaluation of
the derivatives of the elements of
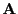 , see the
note 2.4.2.2
, see the
note 2.4.2.2
- bFunc:a procedure that computes the interval evaluation of
the elements of
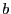 , see the note 2.3.4.3
, see the note 2.3.4.3
- Jbfunc: a procedure that computes the interval evaluation of
the derivatives of the elements of
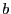 , see the
note 2.4.2.2
, see the
note 2.4.2.2
This procedure will return 1 if the Gauss elimination scheme has been
completed, 0 otherwise.
It will return in general a much more better enclosure than the
classical interval Gauss elimination scheme.
For example consider the system
for 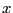 in [3,4] and
in [3,4] and 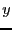 in [1,2]. Using the classical Gauss elimination
scheme the enclosure of the solution is:
in [1,2]. Using the classical Gauss elimination
scheme the enclosure of the solution is:
while if we use the derivatives we get
while the solutions are 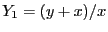 (which has an enclosure of
[1.25,1.666]),
(which has an enclosure of
[1.25,1.666]), 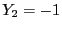 .
.
The ALIAS-Maple procedure LinearBound implements this
calculation.




Next: Regularity of parametric interval
Up: Solving systems of linear
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20