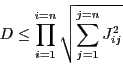
The determinant of a scalar matrix may be calculated with the procedure ALIAS_MRINVD that is also used to determine the inverse of the matrix, see section 7.2.
The determinant of an interval matrix may be calculated by using Gaussian elimination with the procedure
int ALIAS_Det_By_Gaussian_Elim(INTERVAL_MATRIX &B, INTERVAL &DET)This procedures returns 1 if the determinant has been successfully calculated and is returned in DET, 0 otherwise.
There are five main procedures to compute an interval evaluation of the determinant of an interval square matrix:
INTERVAL Slow_Determinant(INTERVAL_MATRIX &A) INTERVAL Slow_NonZero_Determinant(INTERVAL_MATRIX &A) INTERVAL Medium_Determinant(INTERVAL_MATRIX &A) INTERVAL Fast_Determinant(INTERVAL_MATRIX &A) INTERVAL VeryFast_Determinant(INTERVAL_MATRIX &A)These procedures differ only by the computation time (large for the Slow procedure as soon as the dimension of the matrix is larger than 5) and the accuracy of the interval evaluation (which is the worst for the Fast procedure). The Medium_Determinant procedure is a good compromise between efficiency and speed. The procedure Slow_NonZero_Determinant is a special occurrence of the procedure Slow_Determinant which will return as soon it has determined that the interval evaluation of the determinant does not include 0. Note that if the flag ALIAS_Use_Gaussian_Elim_In_Det is set to 1 (the default value being 0), then these procedures will also use the Gaussian elimination to improve the evaluation of the determinant.
There are also special version of the previous procedures:
INTERVAL Slow_Determinant22(INTERVAL_MATRIX &A,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
INTERVAL Medium_Determinant22(INTERVAL_MATRIX &A,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
INTERVAL Fast_Determinant22(INTERVAL_MATRIX &A,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
They differ because the calculation of all the dimensions 2 minors
are computed using the TheDet22 procedure.
The syntax of this procedure is:
INTERVAL TheDet22(INTEGER_VECTOR &ROW,INTEGER_VECTOR &COL,INTERVAL_VECTOR &Input)The integer vectors ROW and COL will have all components equal to 0 except for 2 element, which indicate which rows and columns are used to produce the 2
A more general implementation of the previous procedure is
INTERVAL Determinant22(INTERVAL_MATRIX &A,int Minor,int Row,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
In this procedure Minor indicates the size of the minor that can
be computed using the procedure TheDet22 and Row indicates
if an expansion by row (1) or by column (0) is used.
There are also procedures to compute the derivatives of a determinant
INTERVAL Fast_Derivative_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG); INTERVAL Medium_Derivative_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG); INTERVAL Slow_Derivative_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG);A is a matrix that contain the interval evaluation of the component of the matrix and AG is a matrix that contain the interval evaluation of the derivatives of the components of the matrix. In other words if
If a procedure TheDet22 for calculating the minor is available you may use
INTERVAL Derivative_Determinant22(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG,
int Minor,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
There are also procedures to compute the second order derivatives of a determinant
INTERVAL Fast_Hessian_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG, INTERVAL_MATRIX &AH) INTERVAL Medium_Hessian_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG, INTERVAL_MATRIX &AH) INTERVAL Slow_Hessian_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG, INTERVAL_MATRIX &AH)For a matrix
You may also obtain an upper bound for the determinant of a matrix by using the procedure:
double Hadamard_Determinant(MATRIX &J)where we use the Hadamard bound of the determinant
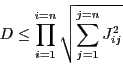
INTERVAL Hadamard_Determinant(INTERVAL_MATRIX &J)
The determinant of a scalar matrix may be calculated with
double Determinant(MATRIX &J)