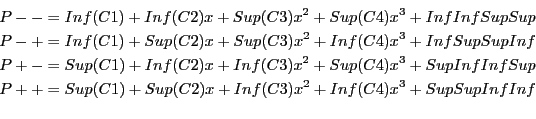Kharitonov polynomials

Kharitonov polynomials are special polynomials that have constant values for their coefficients and are associated to a parametric polynomial. It can be shown that if all the Kharitonov polynomials have the real parts of their roots of the same sign, then all the polynomials in the set will have the real part of their roots of the same sign. For a polynomial $P= \sum C(i)x^{i-1}$ the four Kharitonov polynomials are:

$$\begin{eqnarray*} &&P--=Inf(C1)+Inf(C2)x+Sup(C3)x^2+Sup(C4)x^3+ Inf Inf Sup Sup\... ...&P++=Sup(C1)+Sup(C2)x+Inf(C3)x^2+Inf(C4)x^3+ Sup Sup Inf Inf \\ \end{eqnarray*}$$