



Next: Largest square enclosed in
Up: Possible parameters values for
Previous: Possible parameters values for
Contents
Let consider the parameters space i.e. a  dimensional space
where each of the dimension corresponds to one of the
dimensional space
where each of the dimension corresponds to one of the  parameters.
A point in this space corresponds to a unique value for all the
parameters and therefore to a specific polynomial.
In the parameters space there are possibly a set
parameters.
A point in this space corresponds to a unique value for all the
parameters and therefore to a specific polynomial.
In the parameters space there are possibly a set 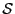 of regions such that
for any point in the region(s) the corresponding polynomial has all
its root within the given interval. The purpose of the following
procedure is to determine an approximation of
of regions such that
for any point in the region(s) the corresponding polynomial has all
its root within the given interval. The purpose of the following
procedure is to determine an approximation of 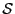 . This
approximation
. This
approximation 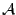 will be constituted of a set of
will be constituted of a set of  dimensional boxes
which are guaranteed to be included in
dimensional boxes
which are guaranteed to be included in 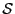 and that will be
written in a file. During the calculation the boxes whose width is
lower than a given threshold
and that will be
written in a file. During the calculation the boxes whose width is
lower than a given threshold 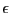 and for which the algorithm
has been unable to determine if they are fully enclosed in
and for which the algorithm
has been unable to determine if they are fully enclosed in 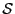 will be neglected. A possible index for measuring the quality of the
approximation
will be neglected. A possible index for measuring the quality of the
approximation 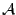 is the ratio
is the ratio 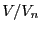 between the total
volume
between the total
volume 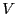 of the boxes
written into the file over the total volume
of the boxes
written into the file over the total volume 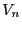 of the boxes that have
been neglected as the volume of
of the boxes that have
been neglected as the volume of 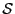 is lower or equal to
is lower or equal to 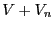 .
.
The procedure is:
int ALIAS_Min_Max_EigenValues_Area(int Degree,int Nb_Parameter,
int Has_Interval,
INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &),
INTERVAL_VECTOR (* TheCoeffCentered)(INTERVAL_VECTOR &,double),
int Nb_Constraints,INTEGER_VECTOR &Type_Eq,
int (* TheMatrix)(INTERVAL_VECTOR &, INTERVAL_MATRIX &),
int Has_Matrix,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
int Has_Gradient,
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL & TheDomain,INTERVAL_VECTOR & TheDomain_Parameter,
int Nb_Points,int Use_Solve,int rand,int Strong,int Iteration,
double Accuracy_Variable,double Accuracy,double AccuracyM,double AccuracyB,
double *Volume_Result,double *Volume_Neglected,double Seuil,
char *FileName,int Has_Input,char *File_Input,
int (* Solve_Poly)(double *, int *,double *),int RealRoot,
INTERVAL_VECTOR (* Evaluate_Complex)(int,int,INTERVAL_VECTOR &),
int (* Simp_Proc)(INTERVAL_VECTOR &))
where the arguments are similar to the one of the previous procedure
except for:
- TheCoeffCentered: a procedure that returns the coefficients
in x of the polynomial P(x+a). Takes as argument the parameters vector
and a
- AccuracyB: the threshold
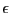 for the maximal width
of the neglected boxes
for the maximal width
of the neglected boxes
- Volume_Result: the total volume of the boxes that have
been determined to be enclosed in the regions
- Volume_Neglected: the total volume of the boxes that have
been neglected
- Seuil: the interval [Seuil[0], Seuil[1]] defines the
allowed range for the real roots of the polynomial
- FileName: the name of the file in which will be written
the boxes that are included in the regions
- Has_Input, File_Input: the purpose of these
variables is to allow an incremental improvement of the
approximation. Indeed after a first run with a given
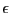 the
quality index may be not satisfactory. It is possible to improve it by
decreasing the value of
the
quality index may be not satisfactory. It is possible to improve it by
decreasing the value of 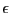 for a second run but it means that
the boxes that have been determined to be enclosed in the region
during the first run will be considered again, thereby leading to a
loss of efficiency. These arguments allow a better control. During the
first run if Has_Input has been set to 1 the neglected boxes
will be stored in the file File_Input. During the second run
(and the subsequent run if needed) Has_Input will be set to 2
and the set of boxes to be considered by the algorithm will be read
from the file File_Input. During this type of run the neglected
boxes will still be written in the file, allowing another run of the
algorithm if needed. Hence the total volume of the boxes enclosed in
the region will be the sum of the Volume_Result while the total
volume of the neglected boxes will be the obtained during the last run
of the algorithm. If Has_Input is set to 3 the neglected boxes
will not be saved in a file.
for a second run but it means that
the boxes that have been determined to be enclosed in the region
during the first run will be considered again, thereby leading to a
loss of efficiency. These arguments allow a better control. During the
first run if Has_Input has been set to 1 the neglected boxes
will be stored in the file File_Input. During the second run
(and the subsequent run if needed) Has_Input will be set to 2
and the set of boxes to be considered by the algorithm will be read
from the file File_Input. During this type of run the neglected
boxes will still be written in the file, allowing another run of the
algorithm if needed. Hence the total volume of the boxes enclosed in
the region will be the sum of the Volume_Result while the total
volume of the neglected boxes will be the obtained during the last run
of the algorithm. If Has_Input is set to 3 the neglected boxes
will not be saved in a file.
- Strong: if 1 we use a secondary algorithm to determine if
for a given box all the polynomial roots are in the range
- RealRoot: 0 if we are considering only real roots, 1 for
the real part of the roots, 2 if we consider polynomial whose roots
are all real and 3 if we consider polynomial with at least one real
root
- Evaluate_Complex(i1,i2,X: let P be the polynomial and
U=P(Seuil_First_Sol[0]+I b), V=P(Seuil_First_Sol[1]+I b). Let
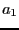 be the real part of U,
be the real part of U, 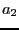 the complex part of U,
the complex part of U, 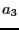 the real
part of V and
the real
part of V and 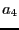 the complex part of V. The procedure will return
in its interval vector the value of
the complex part of V. The procedure will return
in its interval vector the value of 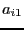 to
to 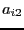 . X
is a Nb_Parameter+1 interval vector, the last one being
the value of b
. X
is a Nb_Parameter+1 interval vector, the last one being
the value of b
This procedure returns the number of boxes written in the result file
or a negative number if the calculation has failed.
The possible negative return code are:
- -2, -3: errors on the bounds for the roots
- -10: Iteration is lower than 10
- other values: the procedure that compute the minima and maximal
real rots in a box has failed




Next: Largest square enclosed in
Up: Possible parameters values for
Previous: Possible parameters values for
Contents
Jean-Pierre Merlet
2012-12-20
![]() dimensional space
where each of the dimension corresponds to one of the
dimensional space
where each of the dimension corresponds to one of the ![]() parameters.
A point in this space corresponds to a unique value for all the
parameters and therefore to a specific polynomial.
In the parameters space there are possibly a set
parameters.
A point in this space corresponds to a unique value for all the
parameters and therefore to a specific polynomial.
In the parameters space there are possibly a set ![]() of regions such that
for any point in the region(s) the corresponding polynomial has all
its root within the given interval. The purpose of the following
procedure is to determine an approximation of
of regions such that
for any point in the region(s) the corresponding polynomial has all
its root within the given interval. The purpose of the following
procedure is to determine an approximation of ![]() . This
approximation
. This
approximation ![]() will be constituted of a set of
will be constituted of a set of ![]() dimensional boxes
which are guaranteed to be included in
dimensional boxes
which are guaranteed to be included in ![]() and that will be
written in a file. During the calculation the boxes whose width is
lower than a given threshold
and that will be
written in a file. During the calculation the boxes whose width is
lower than a given threshold ![]() and for which the algorithm
has been unable to determine if they are fully enclosed in
and for which the algorithm
has been unable to determine if they are fully enclosed in ![]() will be neglected. A possible index for measuring the quality of the
approximation
will be neglected. A possible index for measuring the quality of the
approximation ![]() is the ratio
is the ratio ![]() between the total
volume
between the total
volume ![]() of the boxes
written into the file over the total volume
of the boxes
written into the file over the total volume ![]() of the boxes that have
been neglected as the volume of
of the boxes that have
been neglected as the volume of ![]() is lower or equal to
is lower or equal to ![]() .
.