Evaluation in centered form

The previous procedures may yield sometime to a bad evaluation of the polynomial. For example for the Wilkinson polynomial at order 15 the evaluation for 15.1 leads to 11977410100.791748046875, the correct value being 11977396665.006561033796551. The evaluation obtained when considering that the coefficients and the unknown are intervals is evidently correct and leads to the interval:

 
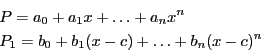
[11977379510.705810546875,11977410100.791748046875]

A better evaluation may be obtained if we use a centered form of the polynomial. Consider the polynomials:

$$\begin{eqnarray*} &&P=a_0+a_1x+\ldots+a_nx^n\\ &&P_1=b_0+b_1(x-c)+\ldots+b_n(x-c)^n \end{eqnarray*}$$

where $c$ is a real. For an appropriate choice of the $b_i$ we may have $P=P_1$ for all $x$. The procedures:

 
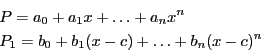
VECTOR Coeff_Polynomial_Centered_Interval(int Degree,VECTOR &Coeff,REAL P);
INTERVAL_VECTOR Coeff_Polynomial_Centered_Interval(int Degree,
                  INTERVAL_VECTOR &Coeff,REAL P);

enable to compute the $b_i$ for the centered form at P either for polynomial or interval polynomial. To take into account numerical errors you may use:

 
INTERVAL_VECTOR Coeff_Polynomial_Centered_Safe_Interval(int Degree,VECTOR &Coeff,REAL P);
INTERVAL_VECTOR Coeff_Polynomial_Centered_Fast_Safe_Interval(int Degree,
           INTERVAL_VECTOR &Coeff,REAL P);

which return safe value for the coefficients (in the second form we assume that you have pre-computed safe value for the coefficients of the polynomial using the procedure described in section 5.9.10).

Then we may use the procedures:

 
REAL Evaluate_Polynomial_Centered_Interval(int Degree,VECTOR &Coeff,REAL Center,REAL P);
INTERVAL Evaluate_Polynomial_Centered_Interval(int Degree,VECTOR &Coeff,INTERVAL P);
INTERVAL Evaluate_Polynomial_Centered_Interval(int Degree,INTERVAL_VECTOR &Coeff,
    REAL Center,REAL P);
INTERVAL Evaluate_Polynomial_Centered_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL P);

These procedures return the evaluation of the polynomial at P using the centered form at Center or at the middle point of P if is an interval. For example for the Wilkinson polynomial at order 15 the evaluation for 15.1 using the centered form at 15 leads to 11977396665.00650787353516 which is largely better than the previous evaluation.