Analyzing the real part of the roots

For some applications it may be interesting to determine if a polynomial in a set defined by a parametric polynomial has the real part of one of its roots equal to a pre-defined value. This may be done by using the procedure

 
int ALIAS_Is_Root_RealPart(int Degree,  
           int NbParameter,
           int HasInterval,
           INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &), 
           INTERVAL_VECTOR (* TheCoeffCentered)(INTERVAL_VECTOR&,double a), 
           int Iteration,
           INTERVAL_VECTOR &Par,
           double *Root,
           INTERVAL_VECTOR (* EvaluateComplex)(int,int,INTERVAL_VECTOR &),
           int (* Simp)(INTERVAL_VECTOR &))

where

Degree: the degree of the polynomial
NbParameter: the number of parameters that appear in the coefficient of the polynomial
HasInterval: 1 if the coefficient include intervals not defined by parameters, 0 otherwise
TheCoeff: a procedure to calculate the coefficients of the polynomial being given range for the parameters
TheCoeffCentered: a procedure to calculate the coefficients of the polynomial
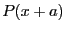
Iteration: the maximum number of box that may be used by the algorithm
Par: the ranges for the parameters
Root: we look for polynomial whose real part of the root is either Root[0] or Root[1]
EvaluateComplex: a procedure that returns 4 intervals. The input interval vector has dimension NbParameter+1 elements, the first one being the parameters, the last one being 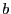. The procedure should evaluate and should return the real part of 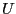, the complex part of 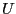, the real part of 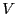and the complex part of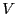
Simp: an optional simplification procedure that returns -1 if the polynomials in a set cannot roots with real part equal to Root[0] or Root[1]

Next: Utilities Up: Analyzing univariate polynomials Previous: Analyzing the real roots

La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de COPRIN

COPRIN home page

La page "Présentation" de l'INRIA

INRIA home page

Jean-Pierre Merlet