



Next: Budan-Fourier method
Up: Descartes Lemma
Previous: Mathematical background
Contents
The syntax of the procedure is:
INT Descartes_Lemma_Interval(int Degree,VECTOR &Coeff)
with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the
polynomial in increasing degree
This procedure returns the number of positive real roots up to an even
number. If the procedure returns 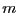 the number of positive roots is
the number of positive roots is
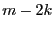 with
with ![$k\in[0,m/2]$](img582.png) .
.
There is an implementation of this method for interval
polynomial. Here it is necessary to introduce an additional parameter
to indicate the confidence we have in the result. The procedure is
implemented as:
INT Descartes_Lemma_Interval(int Degree,INTERVAL_VECTOR &Coeff,int *Confidence);
Confidence is a quality index:
- 1: the result is exact, for all polynomials in the set the
number of positive real roots is
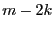
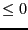 : the number of positive real roots for all the
polynomials
in the set is
: the number of positive real roots for all the
polynomials
in the set is 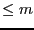
Similar algorithms for negative roots are available:
INT Descartes_Lemma_Negative_Interval(int Degree,VECTOR &Coeff)
INT Descartes_Lemma_Negative_Interval(int Degree,INTERVAL_VECTOR &Coeff,int *Confidence)
Jean-Pierre Merlet
2012-12-20