



Next: Example
Up: Finding bounds on the
Previous: Implementation
Contents
The above algorithms have been regrouped in two procedures, one for
determining the bound on the positive roots, the other for the
negative roots:
int Global_Positive_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);
int Global_Negative_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);
with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the
polynomial in increasing degree
- Bound: the bound on the positive or negative roots
For the positive root if Bound=[a,b] and b=0, then there is no
positive root. Similarly for the negative root is a=0, then there is
no negative root. The procedure returns 0 in case of failure which
correspond to the failure of all the previous algorithms, 1 in case
of success. Note that for Laguerre and Newton method the
maximum number of iteration is defined by the global variable
Max_Iter_Laguerre_Interval fixed by default to 1000.
The step size is defined as:
- if a bound
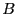 have been previously determined, then the step
size is fixed to
have been previously determined, then the step
size is fixed to 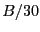 except if the global variable
Step_Laguerre_Interval has been defined to be a double not
equal to 0, in which case this variable is used as the step size.
except if the global variable
Step_Laguerre_Interval has been defined to be a double not
equal to 0, in which case this variable is used as the step size.
- if a bound as not been determined the step size is fixed to 1
except if the global variable
Step_Laguerre_Interval has been defined to be a double not
equal to 0, in which case this variable is used as the step size.
- if the step if lower than the global variable
Min_Step_Laguerre_Interval (which is 0.1 by default) the step
is substituted by Min_Step_Laguerre_Interval
Similar procedure exist for interval polynomial:
int Global_Positive_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower,INTERVAL &Upper);
int Global_Negative_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower,INTERVAL &Upper);
where Lower is an interval on the lower bound: for positive
roots and if Lower=[a,b] then the roots of any polynomial in the
set is greater than a while some polynomial have root greater than
b. Conversely if Upper=[a,b] the roots of any polynomial in the
set is lower than b while some polynomial have root lower than a.
Both procedures for real roots have been regrouped in
void ALIAS_Find_Bound_Polynom(int Degree,
INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &),
INTERVAL_VECTOR &PALL,INTERVAL &Space, INTERVAL &Bound)
where
- PALL: the first component is the bound for the real roots
the polynomial while the following are the value of the parameters for
which the bounds will be obtained
- Space: a default bound for the real roots; may be used to
indicate that we are looking only for bounds on the positive or
negative real roots by specifying a positive or a negative lower bound
- Bound: bounds for the real roots
Subsections




Next: Example
Up: Finding bounds on the
Previous: Implementation
Contents
Jean-Pierre Merlet
2012-12-20